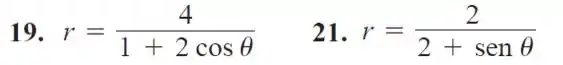Os Exercícios 19-22 fornecem as excentricidades das seções cônicas com um foco na origem do plano de coordenadas polares, com a diretriz para aquele foco. Encontre uma equação polar para cada seção cônica.

Oiii galerinha. Sabemos que a excentricidade para:

• Elipse ;
• Parábola ;
• Hipérbole .

A seguinte equação polar representa uma seção cônica:



As equações que relacionam as coordenadas polares e cartesianas são:



Para a gente entender melhor, vamos observar um exemplo de cada tipo de equação polar:

• Elipse:

Onde .

• Parábola:

Onde .

• Hipérbole:

Onde .