Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 3.2 - Ex. 32
A equação diferencial:
Em que é uma constante positiva, é frequentemente usada como um modelo de uma população sujeita à flutuações sazonais. Encontre e faça um gráfico da solução. Suponha .
Passo 1
Então galera, para resolvermos essa equação diferencial é bem tranquilo, pois basta utilizarmos o método de separação de variáveis, que é o mais de boa que tem! Nossa equação é:
Separando as variáveis:
Integrando ambos os lados, teremos:
E teremos como resultado:
Show!
Passo 2
Para facilitar nossa compreensão vamos simplificar nosso resultado:
Como , teremos:
Então nossa expressão será:
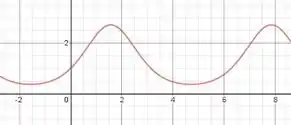
E o gráfico disso é o seguinte:
Resposta
Exercícios de Livros Relacionados
Nos problemas 55-58, encontre uma solução contínua satisfazendo cada equação diferencial e a condição inicial dada.55. d y d x + 2 y = f x ,f x = 1 ,0 ≤ x ≤ 3 0 ,x3 , no qual y 0 = 0 .
Nos problemas 55-58, encontre uma solução contínua satisfazendo cada equação diferencial e a condição inicial dada.56. d y d x + y = f x ,f x = 1 ,0 ≤ x ≤ 1 - 1 ,x1 , no qual y 0 = 1 .
Nos problemas 55-58, encontre uma solução contínua satisfazendo cada equação diferencial e a condição inicial dada.58. 1 + x 2 . d y d x + 2 x y = f x ,f x = x ,0 ≤ x1 - x ,x ≥ 1 , no qual y 0 = 0 .
Resolva 2 x + y y ' = 1 .
Resolvax 2 + 4 d y d x = 2 x - 8 x y sujeito a y 0 = - 1 .