Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 71
A equação pode ser escrita como
Que mostra que o gráfico de pode ser obtido a partir do gráfico de , retendo a parte que está sobre ou acima do eixo e refletindo por esse eixo a parte que está abaixo. Use esse método para obter o gráfico de a partir de .
Passo 1
Bom, o enunciado já nos diz todo o raciocínio da questão. Pois ele explica que o gráfico da função módulo () pode ser obtido a partir do gráfico da função dentro do módulo (), mantendo iguais os valores acima de , mas refletindo pelo eixo todos os valores que estão abaixo desse eixo.
Dessa forma, vamos usar o mesmo raciocínio, o lance é que e, então, . Ok? Então, vamos mexer apenas na parte do gráfico de que está abaixo do eixo , pois vamos refletir essa parte pelo eixo .
Passo 2
O gráfico de é:
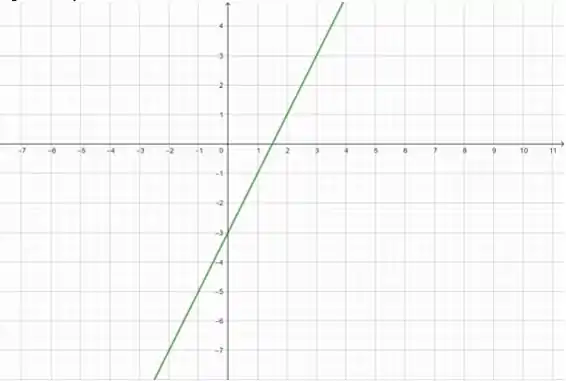
Perceba os valores abaixo do eixo ! Vamos refletir esses valores em torno do eixo :
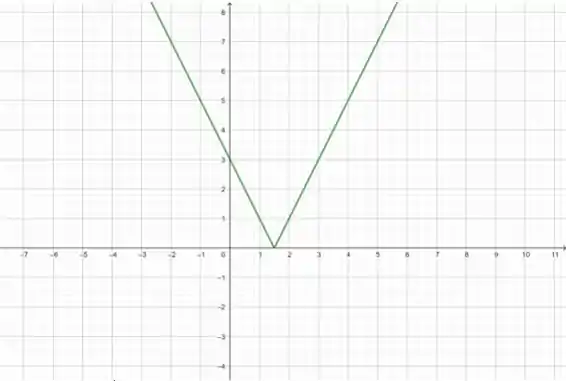
Viu? É só isso! Esse é o gráfico de .
Resposta
