Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 35
Encontre a amplitude e o período e esboce pelo menos dois períodos do gráfico à mão. Confira seu trabalho com um recurso gráfico.
(a)
(b)
(c)
Passo 1
Sendo um gráfico da família dos senos e cossenos, teremos algo com:
Podendo aparecer um cosseno no lugar do seno. Assim, é a amplitude e é dado por !
Passo 2
(a)
Olhando para a equação, podemos ver que , que será nossa amplitude, e
Desenhando 2 períodos do gráfico:
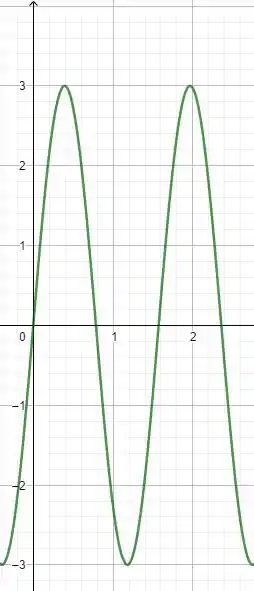
Passo 3
(b)
Olhando para a equação, podemos ver que , que será nossa amplitude (não se preocupe com o sinal negativo na frente, ele não muda nada pra gente aqui), e
Desenhando 2 períodos do gráfico:
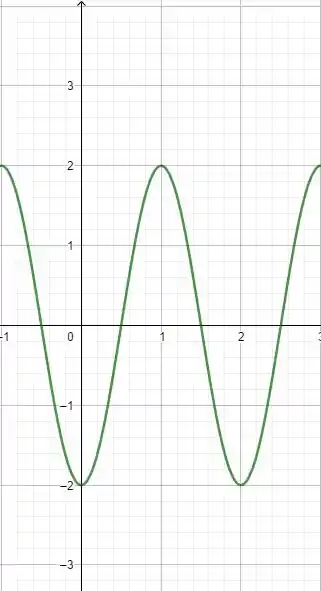
Passo 4
(c)
Olhando para a equação, podemos ver que , que será nossa amplitude, e
Desenhando 2 períodos do gráfico:
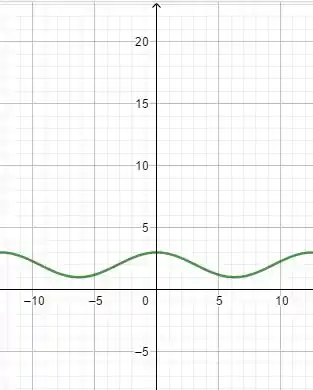
Resposta
(a) ;
(b) ;
(c) ;
Exercícios de Livros Relacionados
(i) Explique por que a função f tem um ou mais buracos em seu gráfico e estabeleça os valores de x nos quais esses buracos ocorrem. (ii) Determine uma função g cujo gráfico seja idêntico ao de f, mas
(i) Explique por que a função f tem um ou mais buracos em seu gráfico e estabeleça os valores de x nos quais esses buracos ocorrem. (ii) Determine uma função g cujo gráfico seja idêntico ao de f, mas
Em 2001, o Serviço Nacional de Meteorologia dos EUA introduziu um novo índice de sensação térmica (WCT). Para uma dada temperatura externa T em graus Fahrenheit e velocidade do vento igual a v milhas
Use a fórmula para o índice de sensação térmica descrita no Exercício 37. W C T = T ,s e0 ≤ v ≤ 3 35,74 + 0,6215 T - 35,75 v 0,16 + 0,4275 T v 0,16 ,s e3v Encontre a temperatura do ar até o grau mais
Use a fórmula para o índice de sensação térmica descrita no Exercício 37. W C T = T ,s e0 ≤ v ≤ 3 35,74 + 0,6215 T - 35,75 v 0,16 + 0,4275 T v 0,16 ,s e3v Encontre a temperatura do ar até o grau mais