Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 14
Esboçar o gráfico da curva dada em coordenadas polares:
Passo 1
Temos que essa curva é do tipo , dada por:
Se é par, temos uma rosácea de pétalas. Neste caso, pétalas e . Assim, o gráfico é dado por:
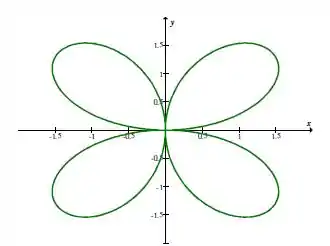
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios 55 e 56, o gráfico da equação dada intercepta a si mesmo. Ache os pontos nos quais isso ocorre.55. r = s e n 3 2 θ
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r =sen 2 θ r = cos 2 θ
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = 4t gθ sen θ r = 4 co
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r = 1 - sen θ r = cos
Nos exercícios de 1 a 6, ache a área da região limitada pelo gráfico da equação dada. 2 . r = 2 - s e n θ