Nos exercícios 55 e 56, o gráfico da equação dada intercepta a si mesmo. Ache os pontos nos quais isso ocorre.
55.
Passo 1
O que o enunciado nos pede é para encontrarmos pontos onde o gráfico da função dada se intercepta com ele mesmo. Para a resolução deste tipo de questão basta fazer o esboço do gráfico da equação e observar no gráfico onde ocorre a intersecção.
Passo 2
Assim, o esboço do gráfico da equação dada é:
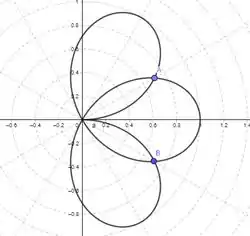
Sendo assim, podemos perceber que os pontos nos quais a equação dada intercepta a si mesmo são .