Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 11
Esboce o campo de direções das equações diferenciais dadas. Use-os para esboçar a curva que passa pelo ponto dado.
11.
Passo 1
Nessa questão, queremos esboçar o campo de direções para a equação . Esta equação nos diz que a inclinação em qualquer ponto no gráfico é igual a diferença entre sua coordenada e o dobro da sua coordenada .
Então para conseguirmos fazer esse desenho, precisamos pegar vários pontos e desenhar pequenos segmentos de reta com inclinação
Note que para qualquer ponto na linha . As inclinações são positivas à esquerda da linha e negativas à direita da linha. Vamos fazer a curva da solução passando pelo ponto , como pede a questão.
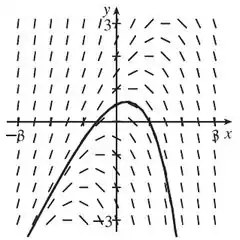
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Desenhe um campo de direções para equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quanto t→∞ . Se esse comportamento depender do valor inicial de y em t = 0, des
Escreva uma equação diferencial da forma d y d t = a y + b cujas soluções têm o comportamento descrito quando t→∞ Todas as outras soluções divergem de y=2
Escreva uma equação diferencial da forma d y d t = a y + b cujas soluções têm o comportamento descrito quando t→∞ Todas as soluções tendem a y=3
Desenhe um campo de direções para equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quanto t→∞ . Se esse comportamento depender do valor inicial de y em t = 0 , de
Desenhe um campo de direções para equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quanto t→∞ . Se esse comportamento depender do valor inicial de y em t = 0 , de