Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.1 - Ex. 15

Os psicólogos interessados em teoria do aprendizado estudam as curvas do aprendizado. Uma curva de aprendizado é o gráfico de uma função P ( t ) , o desempenho de alguém aprendendo uma habilidade como uma função do tempo de treinamento t . A derivada d P d t representa a taxa na qual o desempenho melhora.

  1. Quando você acha que P aumenta mais rapidamente? O que acontece a d P d t quando t aumenta? Explique.
  2. Se M é o nível máximo de desempenho do qual o aprendiz é capaz, explique a razão pela qual a equação diferencial d P d t = k M - P , k uma constante positiva

    3. é um modelo razoável para o aprendizado.

  3. Faça um esboço de uma possível solução da equação diferencial.

Passo 1

  1. P cresce mais rapidamente no início, já que geralmente existem muitas habilidades simples e fáceis de aprender associadas à aprendizagem de uma habilidade. À medida que t aumenta esperamos que d P d t permaneça positivo, mas cresça mais lentamente. Isso acontece porque com o passar do tempo vai sobrando coisas mais difíceis para serem aprendidas.

    2. Passo 2

  2. Perceba que d P d t = k M - P é sempre positiva, pois k é positivo e M é o valor máximo (maior que P ). Então o nível de desempenho de P está aumentando. Quando P se aproxima de M , d P / d t se aproxima de 0 , isto é, os níveis de desempenho diminuem. Então essa equação obedece a nossa explicação do item (a).

    3. Passo 3

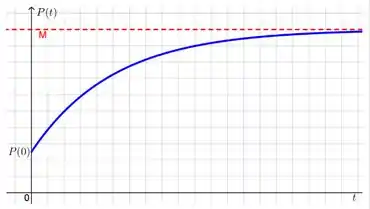
  3. Uma possível solução seria aquela descrita nos itens anteriores: inicia em um valor e vai aumentando rapidamente, após certo tempo diminui seu crescimento até se aproximar de M , como mostra o gráfico:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ligue a equação diferencial a seu campo de direções (I – IV). Dê as razões para sua resposta.3. y ' = 2 - y
Ligue a equação diferencial a seu campo de direções (I – IV). Dê as razões para sua resposta.6. y ' = s e n x s e n y
Use o campo de direções II (acima) para esboçar os gráficos das soluções que satisfazem as condições iniciais dadas. y 0 = 1 y 0 = 2 y 0 = - 1
Faça o esboço de um campo de direções para a equação diferencial autônoma y ' = f ( y ) , onde o gráfico de f é como o exibido. Como o comportamento-limite das soluções depende do valor de y ( 0 ) ?
Esboce o campo de direções para a equação diferencial. Use-o para esboçar três curvas solução. y ' = x 2 - y 2