Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 12
Esboce o campo de direções das equações diferenciais dadas. Use-os para esboçar a curva solução que passa pelo ponto dado.
Passo 1
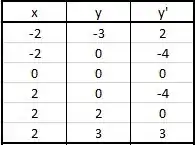
Para esboçar o campo de direções, podemos atribuir valores de e e calcular .O valor de representa a inclinação do campo de direções.
Algumas vezes pode ser necessário utilizar mais pontos pois as inclinações podem variar bastante, assim utilizando mais pontos é garantido que você irá passar por todas as inclinações.
Passo 2
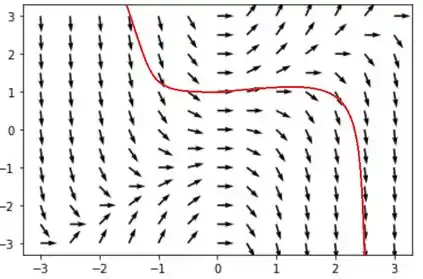
Agora que sabemos como são as inclinações do campo de direção, as curvas soluções são curvas que respeitam essas inclinações e acompanham o campo de direção.
Desta maneira a curva que passa pelo ponto é:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos Exercícios 5 e 6, copie os campos de direção e esboce algumas das curvas integrais. y ' = y + 2 y - 2
Equações IntegraisNos Exercícios 7-10, escreva uma equação diferencial equivalente de primeira ordem e condição inicial y .
Equações IntegraisNos Exercícios 7-10, escreva uma equação diferencial equivalente de primeira ordem e condição inicial y .
Equações IntegraisNos Exercícios 7-10, escreva uma equação diferencial equivalente de primeira ordem e condição inicial y .
Equações IntegraisNos Exercícios 7-10, escreva uma equação diferencial equivalente de primeira ordem e condição inicial y .