Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de r como função de em coordenadas cartesianas.
Passo 1
Sabemos que:
Dessa forma, r alcança seu valor máximo em 2. Esboçando seu comportamento temos:
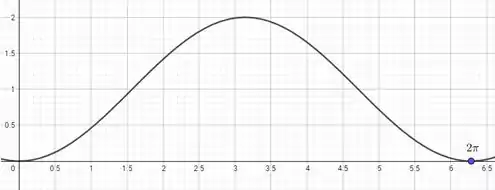
Essa curva representa a seguinte cardioide:
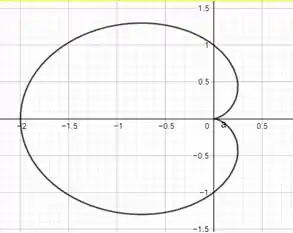
Resposta
Ei, a resposta está no passo a passo :)