Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.1 - Ex. 19
19-22. Calcule, com quatro casas decimais, os primeiros 10 termos da sequência e use-os para traçar o gráfico da sequência com a mão. Esta sequência parece ter um limite? Se assim for, calcule-o. Se não, explique o por quê.
19.
Passo 1
Fala, pessoal! Tudo certinho? Vamos ver como se resolve essa questão:
Resumindo o que a questão pede, basicamente nós teremos que calcular esses 10 primeiros termos de e usá-los para plotar um gráfico, que aqui faremos no software GeoGebra para ficar mais legível.
Depois, precisaremos analisar esse gráfico e tentar identificar se os valores da sequência estão se aproximando de algum valor fixo.
Se sim, isso nos indica que a sequência é convergente e tem um limite, que precisaremos calcular no final para conferirmos se nossa análise incial faz sentido.
Bora lá!
Passo 2
Então pessoal, inicialmente devemos descobrir quanto vale os 10 primeiros termos da sequência. Para descobrirmos isso, basta substituirmos por . Isso é bem tranquilo de fazer, não é mesmo? Sendo assim, teremos:
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Passo 3
Agora que descobrimos os 10 primeiros termos da sequência, vamos colocar esses pontos em um gráfico. Se fizermos isso, teremos:
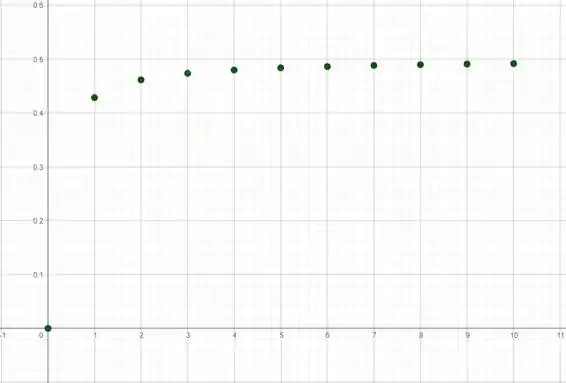
Se observarmos o gráfico com atenção, notaremos que a sequência aparenta se aproximar cada vez mais de , não é mesmo? Então sim, a sequência aparenta ter um limite! Sendo assim, devemos calcular o limite dessa sequência para comprovarmos a observação!
Passo 4
Dividimos o numerador e o denominador pelo maior grau do denominador, que nesse caso é . Fazendo isso, nós simplificamos muito nossa equação ficando com só uma incógnita na nossa sequência, ao invés dessas duas que temos inicialmente. Assim, só precisaremos analisar o comportamento de em um só termo da sequência. Teremos:
Como o limite de tendendo ao infinito é aproximadamente zero, então nosso resultado será:
O limite de uma constante é a própria constante, então:
Sendo assim, fica provado que, de fato, a sequência apresenta uma assíntota em .
Resposta
Nossa sequência tem um limite e é .