Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.1 - Ex. 5
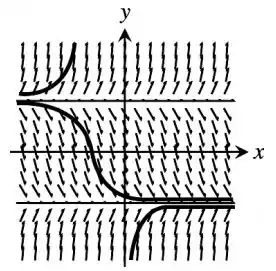
Nos Exercícios 5 e 6, copie os campos de direção e esboce algumas das curvas integrais.
Passo 1
Analisando o desenho do campo de direção, podemos observar que haverá uma reta constante em e .
Além disso, a função é de segundo grau e pode ter a sua concavidade analisada.
Passo 2
Em outros valores, teremos que:
Para a concavidade da equação será positiva;
Para , a equação inverterá a concavidade em ;
Para a concavidade da equação será negativa.
Passo 3
Logo, admitindo essa informações, pode-se fazer o esboço das curvas seguindo as curvas de direção:
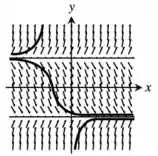
Resposta
Exercícios de Livros Relacionados
Ache a solução completa da equação diferencial dada, determinada pelas condições iniciais (18) d s d t = cos t 2 ; s = 3q u a n d ot = π 3 .
Ache a solução completa da equação diferencial (5) d y d x = 3 x y ² ².
Ache a solução completa da equação diferencial (12) d ² y d x ² = 2 x - 3 ² ² .
Ache a solução completa da equação diferencial (1) d y d t = 4 x - 5 .
Ache a solução completa da equação diferencial (8) d y d x = x ² ( x 3 - 3 ) y ² ² ².