Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 11
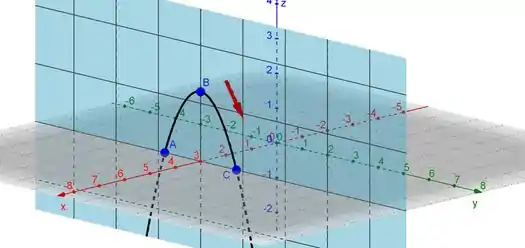
Esboce a curva com a equação vetorial fornecida. Indique uma seta, o sentido na qual aumenta:
Passo 1
Eai? Pessoinha. Tranquilo?
Vamos iniciar está questão entendo o que representa cada termos da equação dada
- O componente é constante e indica que a curva está sempre na posição ao longo de seu percurso.
- O componente varia linearmente com , indicando que a curva se move ao longo do eixo à medida que aumenta.
- O componente é uma função quadrática de , o que influencia a posição ao longo do eixo .
Passo 2
Bom galera, como a gente pode ver, mesmo sendo trididimensional o a linha encontra-se apenas em .
Agora, vamos calcular uma função para a linha através do Passo 1.
A gente substitui por :
Passo 3
Beleza, a função da linha é:
A condição indica que a coordenada da curva é sempre igual a 3. Portanto, estamos restritos a um plano vertical paralelo ao plano onde . A curva descrita por representa uma parábola abrindo para baixo no plano , devido ao termo . À medida que t varia, a altura da curva varia de acordo com essa equação quadrática.
Vamos montar o gráfico:
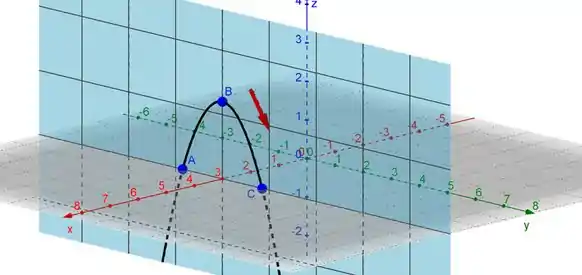
E a seta aponta a o sentido da curva.
Resposta
