Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 20
Esboce o gráfico de cada função e determine se a função tem quaisquer valores extremos absolutos no domínio. Explique a consistência de sua resposta com o Teorema 1.
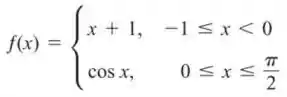
Passo 1
Para verificar se há valores extremos absolutos dessa função dada, podemos aplicar o Teorema 2 e, portanto, aplicar a primeira derivada à função e igualar o resultado a zero.
Para o primeiro intervalo , o Teorema 2 não é aceito por não possuir solução, visto que:
Para o intervalo , o Teorema 2 é aceito e, então:
Passo 2
Analisando esse ponto , temos que é positivo para e é negativo para e, logo, o ponto é um máximo local.
Passo 3
Fazendo o esboço do gráfico, podemos acrescentar ainda que o ponto é um máximo absoluto. Isso se deve ao fato de que o valor da função em é o maior possível dentro do intervalo dado.
Também podemos enxergar que a função possui dois mínimos absolutos em e
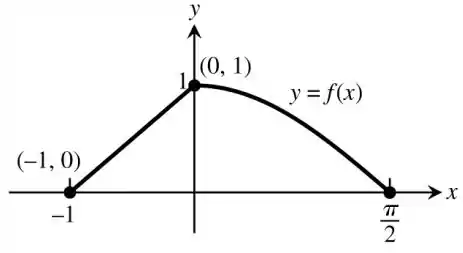
Resposta
As condições do Teorema 1 são atendidas visto que a função está definida em um intervalo fechado e é contínua nele. Para complementar, o Teorema 2 foi útil para encontrar um dos valores extremos absolutos e o gráfico auxiliou na determinação de outros valores extremos absolutos.