Seja:

Explique por que não tem um valor mínimo nem um valor máximo no intervalo fechado .

Então pessoal, a função que nos foi dada no intervalo aberto foi a seguinte:

Nós já sabemos que essa função não possui valores mínimos e máximos porque é uma função afim, ou seja, uma reta. Ademais, nossa é uma função que não possui pontos críticos, que é exatamente a condição de existência de um máximo ou mínimo! O gráfico dessa função é:

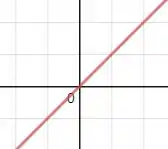
Note que, de fato, no intervalo que nos foi dado não tem picos.

E essa é a nossa resposta, galera! 😉