Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 48
Esboce o gráfico da função
Passo 1
Bom pessoal, temos dois módulos nesta função. Então vamos analisar esses módulos de forma separada e depois fazer a interseção.
A primeira parte sempre será positiva independente do valor de . Da definição de módulo nós temos:
Agora a segunda parte .
Quando o que está dentro do módulo for qualquer valor positivo, o módulo não faz qualquer diferença na função e pode ser tirado. Quando o módulo possui valores negativos, então a gente coloca um símbolo de negativo no módulo. Veja só:
Fazendo os intervalos em função de
Agora temos que fazer a interseção da primeira e da segunda parte, mas vamos fazer isso no passo 2.
Passo 2
Nós temos essas duas funções:
Mas a que estamos procurando é a soma delas:
Então vamos analisar três intervalos:
Quando :
Então:
Quando :
Então:
Quando :
Então:
Juntando tudo:
Passo 3
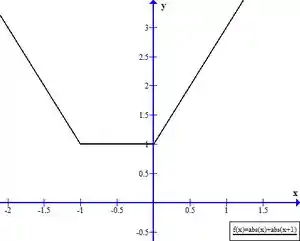
Agora vamos traçar o gráfico:
O primeiro trecho é uma reta decrescente com inclinação -2.
O segundo trecho é uma função constante que vale sempre 1.
E o segundo trecho é uma reta crescente com inclinação 2.
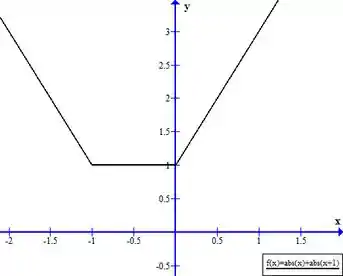
Resposta
