Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 20c
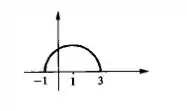
Esboce o gráfico da função dada implicitamente pela equação
Passo 1
Antes de tudo, vamos dar uma olhadinha pra cara dessa equação. Ela é do tipo:
Não é? E essa é a equação de uma circunferência na forma reduzida. Se você não se lembra, dá uma olhadinha na parte de circunferência da nossa plataforma =)
Aqui temos que o centro é dado por e o raio é . Como queremos a parte , queremos apenas a parte positiva da circunferência. Ok? Feita essa parte, vamos ao que interessa?
Primeiro vamos deixar explicitamente em função de . Como? Isolando no lado esquerdo da equação :
Saca só uma coisa aqui: temos duas opções para , uma positiva e outra negativa. Mas e agora, qual escolher? Como dito anteriormente, queremos , então a equação correta é:
Passo 2
Beleza! Determinado isso podemos ver que a função é a parte positiva de um círculo de raio e centro . Os pontos onde a função é zero são:
Essa é uma equação de segunda ordem com e resolvemos ela pela fórmula de Bhaskara:
Sendo assim as raízes são: e .
Então temos que e são as raízes da equação.
E o ponto que afunção cruza o eixo é com :
Então outro ponto pertencente ao gráfico é .
Passo 3
Juntando os pontos que encontramos no passo e sabendo que é a parte de cima de um círculo de raio e centro , podemos fazer o esboço do gráfico:
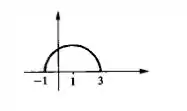
Resposta
