Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 49

Esboce o gráfico da função

f (x) = {[[|x| s e |x| <= 1],[1 s e |x| > 1]])

Passo 1

O enunciado nos pede pra esboçar o gráfico da seguinte função:

f (x) = {[[|x| s e |x| <= 1],[1 s e |x| > 1]])

Repara que a função está dividida em “duas”, então vamos ter que fazer uma avaliação pra cada parte! Partindo pro esboço então!

Passo 2

A primeira parte |x| sempre será positiva independente do valor de x. Temos que ver então para qual intervalo que vale |x|. A condição dada pode ser escrita da seguinte forma:

|x| <= 1 -> - 1 <= x <= 1

Então:

( 1 ) {[[1 >= x >= 0 -> x],[- 1 <= x < 0 -> - x]])

Agora vamos a segunda parte.

Aqui temos que ver apenas quando vale a condição dada:

|x| > 1 -> {[[x < - 1],[x > 1]])

Agora temos que fazer a interseção da primeira e da segunda parte:

Para x < - 1

f (x) = 1

Para x >= 1 :

f (x) = 1

Para - 1 <= x < 0 :

f (x) = - x

Para 0 <= x <= 1 :

f (x) = x

Passo 3

Resumindo:

f (x) = {[[1 s e x < - 1],[- x s e - 1 <= x < 0],[x s e 0 <= x <= 1],[1 s e x > 1]])

Agora vamos traçar o gráfico:

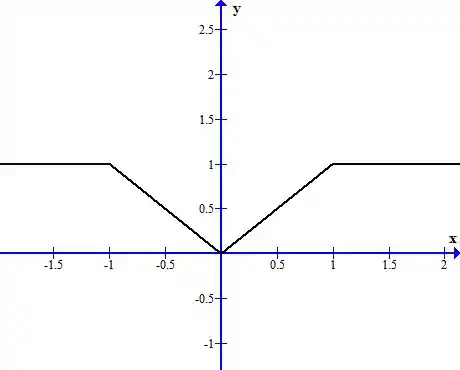
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico:f (x) = ||x| - 1|
Encontre o domínio e esboce o gráfico da função g x = x - x .
Esboce o gráfico da funçãof (x) = |x + 2|
Esboce o gráfico da função g x = x - 1
Esboce o gráfico da funçãog (t) = |1 - 3 t|