Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 46
Esboce o gráfico da função
Passo 1
Bom pessoal, temos um módulo nesta função. E nos é pedido para construirmos o gráfico dessa função.
Então quando o que está dentro do módulo for qualquer valor positivo, o módulo não faz qualquer diferença na função, e pode ser tirado, ficando:
Agora, quando o módulo possui valores negativos, então a gente coloca um símbolo de negativo no módulo. Veja só:
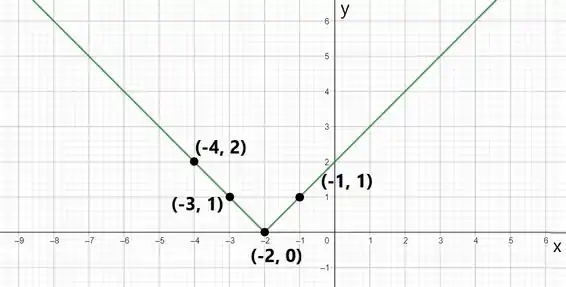
Então, para traçar o gráfico, a gente tem que ter uma atenção ao ponto , que é onde ocorre a mudança de uma função para a outra.
Passo 2
Para esboçar o gráfico, note que ambas as funções nesta função por partes são lineares, então dois pontos de cada uma são suficientes.
Portanto, escolha dois pontos de seus domínios e encontre o valor correspondente da função.
Para a primeira subfunção, dado que o domínio é , escolha, por exemplo, e . Então,
Para a segunda subfunção, dado que o domínio é , escolha, por exemplo, e . Então,
Agora vamos traçar o gráfico:
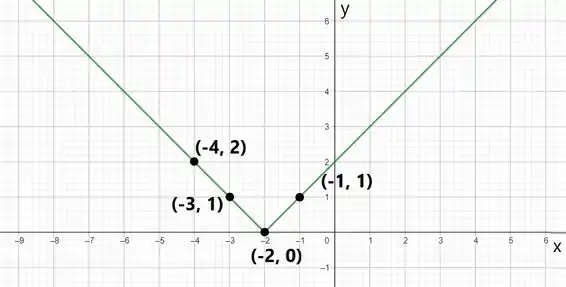
Resposta
