Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 47
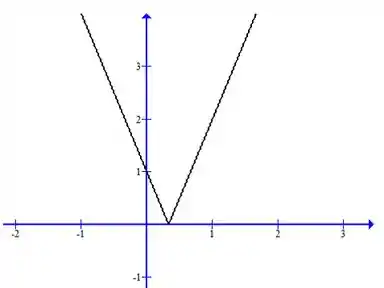
Esboce o gráfico da função
Passo 1
Bom pessoal, precisamos esboçar um gráfico, então vamos la!
Nossa função é um módulo. Então a primeira coisa que eu vou te falar, é relembrar a definição de módulo:
Ou seja, tudo que é negativo fica positivo!
Então aqui a gente tem 2 opções pra abordar essa questão.
- Podemos já usar o módulo pra tornar essa função numa função definida por partes e traçar uma curva pra cada intervalo.
- Ou podemos traçar apenas o gráfico da função no interior do módulo e depois fazer tudo que for negativo ficar positivo.
Eu vou fazer no segundo jeito, porque nessa questão parece mais fácil. Então vamos começar traçando o gráfico de:
Passo 2
Essa função é uma reta:
Pra traçar uma reta, precisamos apenas definir 2 pontos e ligá-los.
E como a gente não é besta, vamos fazer os mais fáceis.
- Quando ,
- Quando ,
Ou seja, a reta conecta os pontos e e seu gráfico fica:
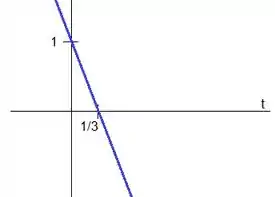
Passo 3
Agora é moleza gente! Se temos o gráfico de
E queremos o seu módulo
É só a gente transformar tudo o que for negativo em positivo, ou seja, espelhar pra cima tudo o que tiver pra baixo do eixo
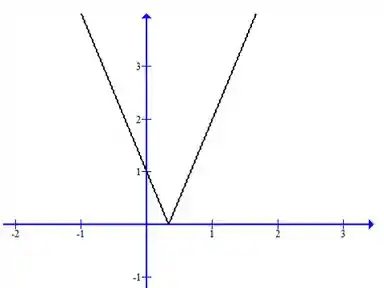
Resposta
