Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.3 - Ex. 24
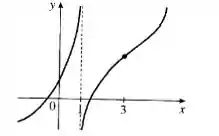
Esboce o gráfico de uma função que satisfaça todas as condições dadas.
para todo , assíntota vertical ,
se ou , se
Passo 1
Eaee, belezinha?? Bom... queremos esboçar o gráfico de uma função que satisfaça todas as condições dadas:
- para todo ;
- assíntota vertical ;
- se ou ;
- se .
Muita coisa ne? Haha
Então vamos analisar cada caso separadamente e, por fim, vamos plotar o gráfico com cada análise que foi feita.
Passo 2
Como para todo e possui assíntota vertical então é crescente em todo o seu domínio e não está definida para .
Passo 3
Como se ou então possui concavidade voltada para cima para valores de menores que e maiores que e como se então possui concavidade voltada para baixo para valores de entre e com ponto de inflexão em .
Passo 4
Portanto, temos o seguinte gráfico:
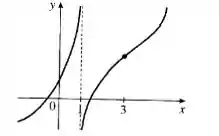
Resposta
Exercícios de Livros Relacionados
Seja f x = x 5 - x 4 - 3 x 3 + 2 x + 4 x 7 - 2 x 6 - 3 x 5 + 6 x 4 + 4 x - 8 (a) Use um CAS para fatorar o numerador e o denominador de f e use os resultados para determinar a localização de todas as
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)