Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 50

Seja

f x = x 5 - x 4 - 3 x 3 + 2 x + 4 x 7 - 2 x 6 - 3 x 5 + 6 x 4 + 4 x - 8

(a) Use um CAS para fatorar o numerador e o denominador de f e use os resultados para determinar a localização de todas as assíntotas verticais.

(b) Confirme que sua resposta está de acordo com o gráfico de f

Passo 1

(a)

Usando um recurso computacional, fatoramos a nossa expressão e chegamos que:

f x =   ( x - 2 ) ( x - 2 ) ( x + 2 ) ( x 2 + x + 1 ) x - 2 x 2 + 1 [ ( x - 2 ) ( x + 2 ) ] 2

Simplificando:

f x =   ( x 2 + x + 1 ) x 2 + 1 ( x - 2 ) ( x + 2 )

Passo 2

Para as assíntotas verticais vamos olhar pro domínio da nossa função:

f x =   ( x 2 + x + 1 ) x 2 + 1 ( x - 2 ) ( x + 2 )

Para evitar que o nosso denominador zere, vamos quere que x não atinja alguns valores, por exemplo:

x 2 + 1 ≠ 0           ∴           x 2 ≠ - 1             ( o k )

x 2 - 2 2 ≠ 0           ⇒         x 2 ≠ 2           ∴             x   ≠ ± 2    

Passo 3

Vamos agora fazer os limites de x   tendendo exatamente pra esses caras, caso nosso limite vá pra mais ou menos infinito, acharemos uma assíntota:

lim x _ → ∓ 2 ⁡       f x = l i m x _ → ∓ 2   ( x 2 + x + 1 ) x 2 + 1 ( x - 2 ) ( x + 2 )

Colocando esse valor dentro da nossa expressão, teremos:

Para   x → 2

l i m x → 2   ( x 2 + x + 1 ) x 2 + 1 ( x - 2 ) ( x + 2 ) = ( 2 2 + 2 + 1 ) 2 2 + 1 ( 2 - 2 ) (   2 + 2 )  

⇒ ( 3 + 2 ) 3 ( 0 ) ( 2 2 ) = 3 + 2 0 = ∞

Maneiro, achamos uma assíntota vertical em x = 2

Para x → - 2

l i m x → 2   ( x 2 + x + 1 ) x 2 + 1 ( x - 2 ) ( x + 2 ) = ( ( - 2 ) 2 - 2 + 1 ) ( - 2 ) 2 + 1 ( - 2 - 2 ) (   - 2 + 2 )  

⇒ ( 3 - 2 ) 3 ( - 2 2 ) ( 0 ) = 3 - 2 0 = ∞

Opa, achamos outra assíntota em x = - 2

Passo 4

(b)

Por recuso computacional, temos que o gráfico de f ( x ) é:

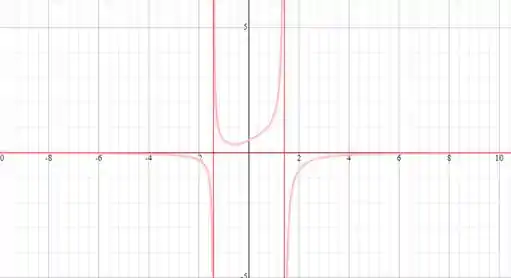
Assíntotas nos mesmos lugares, então estamos de acordo com o gráfico 😊

Resposta

(a) x = 2     e   x = - 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se f x = x + s e n x , prove que f não tem extremos relativos, mas que o gráfico de f posui retas tangentes horizontais. Faça um esboço do gráfico para x ∈ [ - 2 π , 2 π ] .
Se y = 2 x 2 - 3 , (a) ache d y e Δ y para x = 2 e Δ x = 0,5 . (b) Trace um esboço do gráfico e indique os segmentos de reta cujo comprimento são d y e Δ y .
Para certa mercadoria de que x unidades são demandadas semanalmente quando p é o preço de cada unidade, 10 6 p x = 10 9 - 2 ⋅ 10 6 x + 18 ⋅ 10 3 x 2 - 6 x 3 . O custo médio de produção de cada unidade
Nos exercícios de 13 a 32, faça um esboço do gráfico da função f dada, determinando primeiro o seguinte: os extremos relativos de f; os pontos de inflexão do gráfico; os intervalos nos quais f é cresc
Suponha que f e g sejam funções que satisfaçam as hipóteses do teorema do valor médio em [ a ,b ] . Além disso, suponha que f ' x = g ' ( x ) para todo x no intervalo aberto ( a ,b ) . Prova que f x -