Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.5 - Ex. 56
Encontre . Verifique se sua resposta é razoável comparando os gráficos de e .
Passo 1
Bom galera, nesse exercício iremos derivar a nossa função em relação a e iremos traçar o gráfico da função e da sua derivada com o objetivo de verificar se a resposta está correta.
Passo 2
Primeiramente, iremos derivar . Veja que é composta pelo produto de duas funções e que dentro da há uma função de . Dessa forma, deveremos utilizar a regra do produto de funções, que ocorre da seguinte maneira
E a regra da cadeia, onde após derivar a deveremos derivar a função presente dentro da e multiplicar a derivada pela derivada da raiz. Derivando temos
Veja que fora dos parênteses há a função que não está sendo derivada mas que deve ser multiplicada devido a regra do produto. Em , há a derivada que vem devido a regra da cadeia da . Podemos simplificar a derivada, ficando com
Passo 3
Podemos esboçar o seguinte gráfico
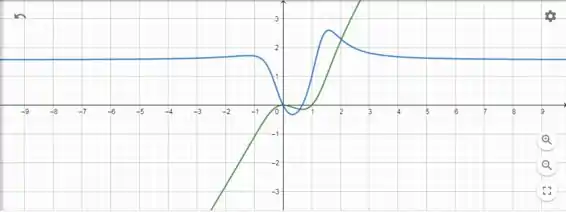
Onde a função verde é e a função azul é .
Resposta
Podemos concluir que a resposta da derivada é razoável com base no gráfico feito. Podemos concluir isso pois quando , o gráfico de possui uma tangente horizontal. Além disso, quando está diminuindo, é negativa e quando está aumentando é positiva.