Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 20
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
De inicio, vamos representar o gráfico:
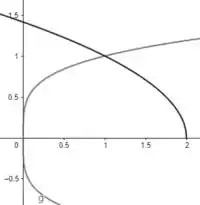
Fazendo a interseção das equações, podemos reorganizar os termos. A função pode ser:
Ou...
Assim, substituindo na primeira equação:
Podemos escrever também da seguinte forma:
Esse será o nosso intervalo de integração. Agora podemos calcular a área!!
Passo 2
Resolvendo essa integral:
Então,
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da