Esboce a região de integração e mude a ordem de integração.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
É possível observar que estamos trabalhando com uma região do tipo . Pois estamos integrando inicialmente em .
O domínio da mesma é:
Passo 2
Agora que determinamos a nossa região, podemos esboça-la. Portanto:
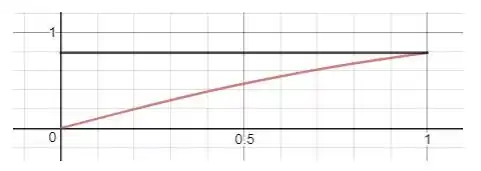
Passo 3
Agora que esboçamos a região de integração, vamos mudar sua ordem de integração.
Sabemos que a região é limitada inferiormente pela reta e superiormente por . Para os limites laterais temos, à esquerda e à direita. Portanto: