Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 49
Esboce a região de integração e mude a ordem de integração.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos resolver essa questão mudando a ordem de integração da integral dupla dada. Para isso, precisamos esboçar a região de integração e identificar os limites apropriados para a nova ordem.
Primeiro, é importante entender que estamos trabalhando com uma região do tipo , onde integramos inicialmente em relação a .
Uma região do tipo no plano é uma região onde está entre duas funções de , e varia entre dois valores constantes. Mais formalmente, uma região é do tipo se ela pode ser escrita como:
Onde e são constantes, e e são funções contínuas de .
No nooso caso, a integral dada é:
Vamos identificar os limites de integração:
- Para :
- Para :
Passo 2
Agora, vamos esboçar a região de integração. A região é delimitada por , , e .
Para isso, observe que:
- A curva é uma função logarítmica que cresce conforme aumenta.
- No intervalo , a curva começa em e vai até .
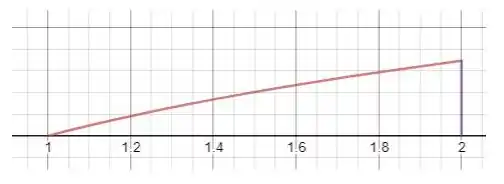
Portanto, nossa região de integração é a área entre a reta e a curva desde até .
Passo 3
Agora que temos a região esboçada vamos determinar os novos limites de integração, para trocar a ordem da integral.
Para reescrever a integral, integramos primeiro em relação a e depois em relação a .
- O valor de varia de a (altura da região).
- Para um valor fixo de , varia de (a inversa de até .
Portanto, a nova integral será: