Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 39
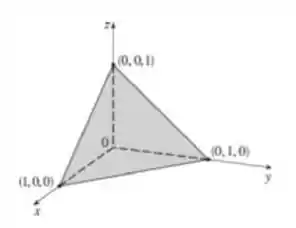
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
Fala, galera! Como vocês estão?
Vamos entender o que nossa questão pede. Ela nos dá a integral dupla:
E quer que a gente esboce o volume que essa integral está descrevendo. Isso é um gráfico de um sólido e vamos precisar usar um software para gerar esse gráfico, como o Geogebra.
Primeiro, vamos usar os limites de integração da nossa integral para entender em qual região no plano essa integral está sendo calculada, e plotar o gráfico dessa região.
Depois vamos olhar o integrando, que vai ser a função:
que vai delimitar nosso volume, já que a integral dupla de uma função é o cálculo do sólido abaixo dela na região .
Vamos juntos!
Passo 2
Vamos olhar primeiro para o domínio de integração. Enquanto varia de até , varia da reta até . Assim, o domínio é representado por:
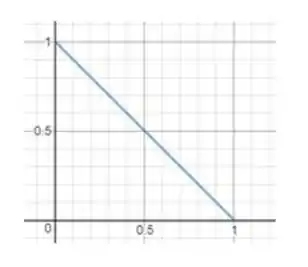
Pronto, encontramos nossa região .
Passo 3
Agora vamos olhar para o integrando. Podemos encarar
Essa é equação de um plano. Vamos entender onde esse plano intercepta cada plano.
- Para , no plano
- Para , no plano
- Para , no plano
- Para .
- Para .
- Para .
Isolando :
Temas as retas que delimitam o sólido em cada plano. Agora podemos achar seus pontos de interseção com cada eixo:
Assim o sólido pode ser descrito por:
Trata-se de um tetraedro com vértices na origem e nos pontos e :
