Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 10
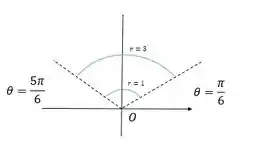
Esboce a região no plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas.
Passo 1
Fala galera! Vamos para mais uma questão?
Para esboçar a região no plano que consiste em pontos cujas coordenadas polares satisfazem e , podemos seguir os seguintes passos:
A desigualdade significa que o raio varia de a , ou seja, os pontos estão dentro de um círculo com raio máximo de e mínimo de em coordenadas polares.
A desigualdade indica que o ângulo 𝜃 varia de a , o que corresponde a um setor angular no plano.
Passo 2
Esboçar o setor angular:
- Marque os ângulos e no círculo unitário (raio ).
- Trace linhas radiais partindo da origem (ponto central) até os pontos correspondentes a esses ângulos.
- A região delimitada por essas linhas radiais dentro do círculo unitário é o setor angular que corresponde à condição
- Trace um círculo interno com raio e um círculo externo com raio .
- A região entre esses dois círculos representa a condição .
Passo 3
A região no plano que satisfaz simultaneamente e é a interseção da região delimitada pelo setor angular e os anéis circulares.
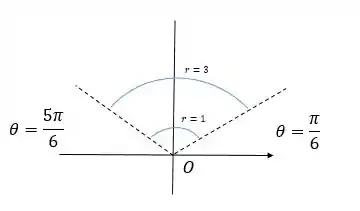
Resposta
