Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.5 - Ex. 51
Estima-se que um operário de uma oficina que fabrica molduras para quadros possa pintar y molduras, x horas após ter começado a trabalhar às 8 da manhã, e
Ache o momento em que o operário está trabalhando mais eficientemente (isto é, em que instantes ele atinge o ponto de diminuição do retorno?).
Passo 1
Se representa quantas unidades de moldura foram feitas após horas de trabalho, então é a taxa de variação de em relação a . O ponto de diminuição do retorno é o ponto onde o operário está produzindo com maior eficiência, e é um ponto de inflexão do gráfico.
Sendo assim, nós precisamos achar o ponto onde
Igualando a 0:
Analisando a direção da concavidade:
Quando , temos 2 horas e 40 minutos depois das 8 horas.
Desenhando o gráfico da função para comprovarmos o que foi visto:
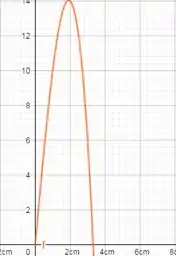
Resposta
O trabalhador está produzindo com maior eficiência às 10 horas e 40 minutos.