Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 36
Este exercício explora o efeito da função interior sobre a função composta .
a) Faça o gráfico da função usando a janela por . Qual a diferença entre esse gráfico e o da função seno?
b) Faça o gráfico da função usando a janela por . Qual a diferença com esse gráfico e o da função seno?
Passo 1
Olá, meu brother. Vamos de resolução.
Aqui a gente precisa analisar o comportamento que a função interior tem em relação a uma funçã composta:
Em janelas que nos são dadas.
Mas que janela é essa??
Então... quando a gente olha um gráfico, a gente quer tirar todas as informações que estão contidas nele. E, para isso, o gráfico não pode estar nem grande demais para o plano cartesiano e nem pequeno demais.
O tamanho ideal é aquele que contém o máximo de informações possíveis que podemos extrair do gráfico. Para isso, precisamos calcular pontos chaves que nos dirão o tamanho correto da janela.
Para o plot dos gráficos a gente vai utilizar o GeoGebra. Ele é online e gratuito e super fácil de utilizar.
Passo 2
No item (a) devemos esboçar o gráfico da função na janela considerada:
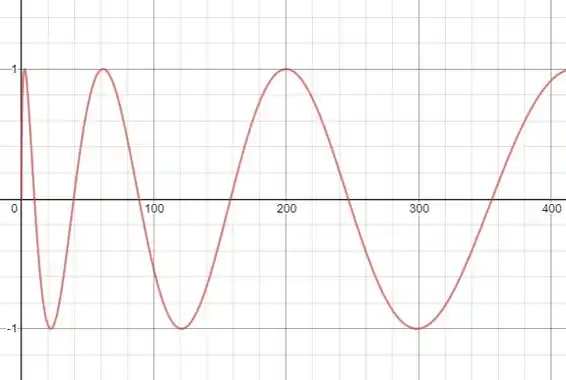
A curva lembra um pouco a função seno, porém nesse caso o período de oscilação aumenta conforme aumenta.
Passo 3
No item (b), a função passa a ser :
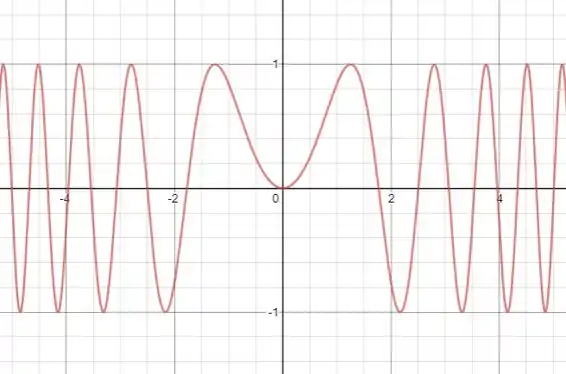
O domínio de e é o conjunto dos números reais.
) não é uma função periódica como . oscila mais frequentemente do que quando aumenta.
Enquanto o gráfico de é simétrico em relação à origem (função ímpar), é simétrico em relação ao eixo vertical (função par).
Resposta
Esboço de gráfico.