Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 31
Faça o gráfico da função para vários valores de . Como mudará o gráfico quando varia?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente esboçar o gráfico da função para vários valores de e explicar como a variação do valor de muda esse gráfico.
Pra entender como altera a forma do gráfico, vamos precisar fazer o gráfico de uma família de funções, que é uma coleção de funções cujas equações estão relacionadas. E pra fazer isso, vamos precisar atribuir alguns valores para .
Então, vamos chamar , substituir esses valores da equação e plotar os gráficos correspondentes, pra a partir daí verificar a influência de no formato da curva.
Lembrando que, nesse caso, é um polinômio de grau , então a curva terá um formato mais ou menos parecido com o de uma parábola, por conta do expoente par, beleza? Além disso, por se tratar de um polinômio, ela pode assumir qualquer valor real.
Vamos lá!
Passo 2
Vamos começar fazendo na função, assim vamos ter:
Beleza, agora vamos substituir e :
Da mesma forma, para , teremos:
Para , temos:
Para , temos:
E para , vamos ter:
Beleza! Agora vamos plotar essas funções para ver como a curva se altera.
Passo 3
Com o auxílio de um software, usando as diferentes funções para os diferentes valores de que calculamos no passo anterior, vamos ter:
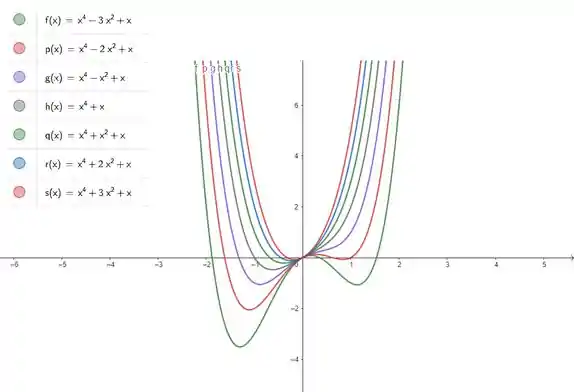
Vemos que para positivo () conforme seu valor cresce, a curva vai se aproximando cada vez mais de uma parábola, pois o termo quadrático predomina.
Para (negativo), vemos que o formato da curva é alterada com a tendêncida de formação de dois “poços” que serão mais profundos quanto mais negativo for . Então, ele altera os pontos de mínimo da função e as raízes do polinômio, que são os pontos onde a curva corta o eixo .
Valeu, galera! Até a próxima! 😉
Resposta
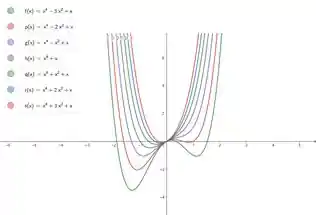
altera os pontos de mínimo do gráfico, à medida que se torna mais negativo e altera a amplitude da curva à medida que se torna mais positivo.