1. Queremos encontrar uma equação diferencial que descreva o resfriamento de uma xícara de café a C em uma sala com temperatura de que resfria a uma taxa de quando sua temperatura é de . Vamos lembrar que a taxa de resfriamento de um corpo quente é proporcional à diferença de temperatura com o ambiente, temos a equação descrevendo a variação de temperatura. O que precisamos fazer agora é coletar os dados da questão e substituir nessa equação.

Como a taxa de resfriamento é = -1. O sinal negativo aparece porque a temperatura está diminuindo.

Quando , ficamos com:

Então a equação que a gente queria encontrar é

Passo 2

2. Queremos desenhar um campo de direções e usá-lo para esboçar uma solução para o nosso problema. Sabemos que conforme o tempo aumenta, a taxa de diminuição da temperatura diminui, então podemos desenhar:



Para esboçar a curva que representa nossa solução, podemos marcar nosso ponto inicial (quando ) e traçar o resto do gráfico seguindo o campo de direções. Assim:



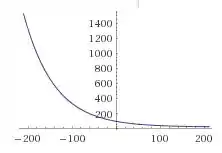
Passo 3

Agora queremos achar o valor limite da temperatura. Mas como encontramos ele? Fazendo ! Então:

Assim, descobrimos que a temperatura limite é .

Passo 4

3. Queremos estimar a temperatura do café após minutos, usando o método de Euler, com passo .

Para começar, vamos lembrar o que diz o método de Euler:

Sabemos que inicialmente, nossa xícara tinha temperatura igual a , então

Precisamos calcular então vamos usar a fórmula várias vezes até alcançar nosso objetivo.

Substituindo

Agora vamos fazer

Mais uma vez...

Agora,

Ufa, última vez!