Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 27
A figura mostra um circuito contendo uma força eletromotriz, um capacitor com capacitância de Farads (F) e um resistor com resistência de ohms (Ω). A queda de voltagem no capacitor é onde é a carga (em coulombs); nesse caso a Lei de Kirchhoff fornece
Mas de modo que temos
Suponha que a resistência seja , a capacitância seja e a pilha forneça uma voltagem constante de V.
- Desenhe um campo de direções para essa equação diferencial.
- Qual é o valor-limite da carga?
- Existe uma solução de equilíbrio?
- Se a carga inicial for use o campo de direções para esboçar a curva solução.
- Se a carga inicial for use o método de Euler com o passo para estimar a carga depois de meio segundo.
Passo 1
- Queremos desenhar um campo de direções para a equação diferencial . Vamos substituir os dados que temos: , V.
- Precisamos encontrar o valor-limite da carga. Quando a carga no capacitor se aproxima do valor limite de carga, a carga não mudará mais. Então temos que
- Temos uma solução de equilíbrio quando
- Para desenhar a solução de equilíbrio quando a carga inicial for basta pegarmos o campo desenhado no item a e desenhar uma linha seguindo as direções a partir do ponto inicial, assim:
- Queremos estimar a carga depois de meio segundo, através do método de Euler, quando a carga inicial for
Isso quer dizer que em cada ponto que pegarmos, teremos uma reta com inclinação igual a , assim, podemos pegar vários pontos e desenhar pequenos segmentos de reta. Desse jeito:
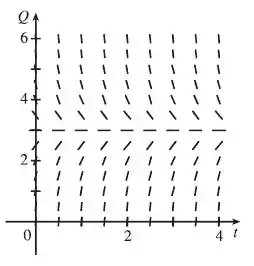
Passo 2
Substituindo na fórmula, ficamos com:
Coulombs
Passo 3
Então:
Coulombs
é a solução de equilíbrio
Passo 4
Passo 5
Sabemos que
Também sabemos que então
Então vamos aplicar a fórmula do método de Euler até chegarmos em
Resposta
(b) 3 Coulombs
(c)
(d)