Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 23
No exercício a seguir, ache a equação da hipérbole com as propriedades dadas e faça um esboço do gráfico.
Focos em (-5,1) e (1,1) e um vértice em (-4,1)
Passo 1
É importante nessa questão, a gente fazer alguns esboços durante as resoluções, vai nos dá um bom norte sobre as equações! A primeiro momento, a gente percebe que os focos estão no mesmo eixo (eixo x), portanto a hipérbole tem um formato parecido com esse:
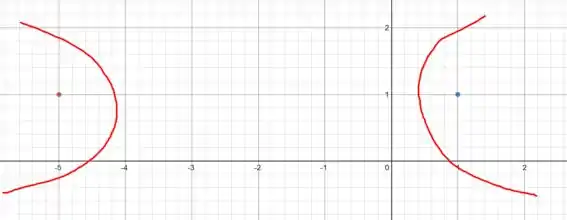
A questão também nos dá que existe um vértice em (-4,1), que fica no lado esquerdo da nossa hipérbole. E isso é absolutamente INCRIVÉL!! Sabe porquê? Porque a gente vai saber a distancia do foco até o vértice!
1
Se essa é a distância de um foco para um vértice de um lado, essa mesma distância vale para o outro foco:
1
Logo,
Com isso obtemos a distância entre os vértices com uma simples subtração, que é igual ao famoso 2a.
Legal, temos que:
Passo 2
Olhe só!! Temos o nosso primeiro valorzinho importante na equação, que é o a. E apesar de não ter citado, temos ainda o valor de c, que corresponde a metade da distancia focal.
Portanto:
EEEEITA! Estamos quase lá! Está falando somente um valorzinho para irmos para o passo final: o valor de b. Para acha-lo, vamos para essa equação que está relacionada com a hipérbole:
Ah gente agora é so partir pro abraço né? Tá muuuito fácil!
Passo 3
Temos os valores de a,b e c!! Melhor que isso só um 10 na próxima prova (que você vai tirar achando os valores de a,b e c kkkk. Vamos ao que importa: a equação canônica da hipérbole para o nosso caso (focos pararelos ao eixo x e fora da origem)
Em que Xc e Yc correspondem respectivamente as coordenadas x e y do centro da hibérbole. Pelas informações que a gente já tem, sabemos que o nosso centro fica na posição (-2,1), isso porquê o centro fica no meio dos vértices, e com as nossas coordenadas é fácil de enxergar isso. Portanto nosso Xc = -2 e nosso Yc = 1. Vamos montar a equação e nos livrar dessa questão? SIMBORA!
Organizando os dados: a = 2 , b = , Xc = -2, Yc = 1.
Logo, a nossa equação é:
Fazendo o esboço, fica: