Nos exercícios de 11 a 22, a equação é de uma cônica tendo um foco na origem. Em cada exercício, (a) ache a excentricidade, (b) identifique a cônica, (c) escreva a equação da diretriz que corresponde ao foco na origem, (d) faça o esboço da curva.
13.
Passo 1
Para responder o que está sendo pedido no enunciado, basta observar a equação da cônica dada e vê se ela se enquandra em alguma das equações do teorema 10.8.3. Caso ela não se enquadre, basta realizar algumas operações básicas para transformar a equação dada numa equação da forma escrita pelo teorema.
Passo 2
Sendo assim, temos para a cônica em questão:
A equação da diretriz é dada por:
Passo 3
Um esboço da curva pode ser representado por:
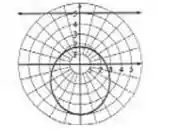
Resposta
- /2
- Elipse
- gráfico