Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.2 - Ex. 5
Nos exercícios de 1 a 16, ache o centro, vértices, focos e extremidades do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos.
Passo 1
Vamos começar deixando a nossa equação no formato da equação da elipse, e para isso precisamos dividir todos os termos por .
Assim já conseguimos a primeira informação pedida, nossa elipse possui o centro na origem .
Passo 2
Da equação da elipse temos que e , ou seja, e
Assim, os vértices são os pontos: e
E as extremidades do eixo menor (eixo y) estão nos pontos: e
Passo 3
Nosso último passo temos que fazer o esboço, mostrando os focos. Então, vamos achar os focos através de:
Ou seja...
Os focos são: e
Passo 4
Nosso esboço é:
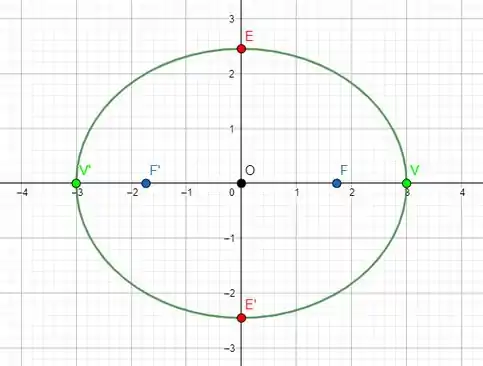
Resposta
Centro:
Vértices: e
Extremidades: e
Focos: e
Exercícios de Livros Relacionados
São dados, em cada caso, o parâmetro geométrico a e os focos de uma elipse. Obtenha uma equação algébrica de segundo grau em x e y que todo ponto x , y da elipse deva satisfazer. a = 4 F 1 = - 3,2 F 2
Nos casos em que a equação dada descreve uma elipse de focos em algum dos eixos coordenados, especifique-o e calcule: a distância focal, a medida do eixo maior e a medida do eixo menor. Faça alguns es
Escreva uma equação reduzida da elipse, nos casos:O centro é O , os focos estão em O x , o eixo menor mede 6, e a distância focal é 8.O centro é O , os focos estão em O y , o eixo maior mede 10, e a d
Nos casos em que a equação dada descreve uma elipse de focos em algum dos eixos coordenados, especifique-o e calcule: a distância focal, a medida do eixo maior e a medida do eixo menor. Faça alguns es
Nos casos em que a equação dada descreve uma elipse de focos em algum dos eixos coordenados, especifique-o e calcule: a distância focal, a medida do eixo maior e a medida do eixo menor. Faça alguns es