Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.4 - Ex. 18
Nos Exercícios de 3 a 22, simplifique a equação dada com uma rotação e uma translação de eixos. Faça um esboço do gráfico e mostre os três conjuntos de eixos.
18.
Passo 1
Galera, para rotacionarmos os eixos, devemos seguir o seguinte teorema, segundo o Leithold na seção 10.4:
“Se for a representação de um ponto em relação a um conjunto de eixos e for a representação de após a rotação dos eixos de um ângulo , então:
No qual pode ser determinado utilizando-se a seguinte expressão:
Aqui vale ressaltar que é o termo que acompanha , é o termo que acompanha e é o termo que acompanha em uma equação de cônica, que é dada da seguinte maneira:
Uma vez que esses conceitos estão claros pra gente, então podemos começar os trabalhos! Vamo que vamo!
Passo 2
A equação que nos foi dada é:
De ínicio, precisamos determinar e , certo? Segundo a equação acima, temos que , e . Sendo assim, temos:
Portanto:
Utilizando as identidades trigonométricas, teremos:
Agora que determinamos e , substituindo nas equações após a rotação de eixo, teremos:
Passo 3
Agora que encontramos as expressões para e pós rotação de eixos, vamos substituir os novos valores na equação dada, se liga:
Abrindo e fazendo as devidas simplificações, obteremos:
Dividindo todos os membros por , teremos:
Chamando e , teremos:
Por fim, esboçando o gráfico, teremos:
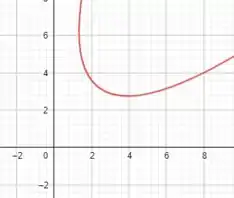
Resposta
