Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 51
Para os Exercícios 51-54 encontre o ângulo , onde .
51.
Passo 1
Se tirarmos a raiz quadrada dos dois lados da equação chegamos direto na resposta:
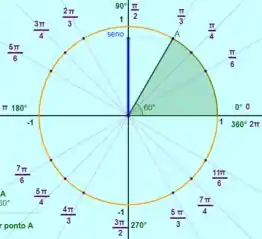
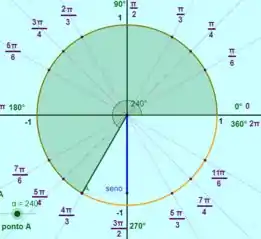
Esse é o valor de um dos ângulos notáveis, o . Notemos também que existem outros valores de possível, , e :
Resposta
Exercícios de Livros Relacionados
No exercício a seguir é dado um dos valores de s e nx , cos x e t gx . Determine os outros dois valores quando x está no intervalo especificado. t gx = 2 ,x ∈ [π , π 2]
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? s e n( 2 x )
No exercício a seguir é dado um dos valores de s e nx , cos x e t gx . Determine os outros dois valores quando x está no intervalo especificado. s e nx =3 5 ,x ∈ [π 2 , π]
No exercício a seguir é dado um dos valores de s e nx , cos x e t gx . Determine os outros dois valores quando x está no intervalo especificado. c o sx =- 5 13 ,x ∈ [ π 2 , π]
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? s e nx -π 4 + 1