Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.Revisão - Ex. 66

Nos exercícios de 63 a 68, defina f   ο   g e determine os números nos quais f   ο   g é contínua.

66) f x = x + 1 ; g x = 1 x - 3

Passo 1

Nós queremos obter a função composta f   o   g = f ( g x ) . Para isso substituiremos a função g ( x ) na função f ( x ) .

f g x = g ( x )

f g x = 1 x - 3 + 1

Tirando o MMC, temos:

f g x = x - 2 x - 3

Passo 2

Agora precisamos determinar os números para os quais f g x   é contínua.

O domínio de f ( g x ) será o conjunto de todos os números reais, tais que

x - 2 x - 3 ≥ 0

Resolvendo a inequação quociente, temos:

x - 2 = 0

x = 2

x - 3 = 0

x = 3

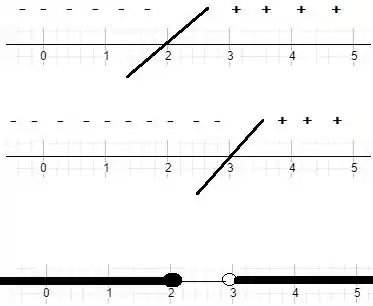
isto é todos os números no intervalo - ∞ , 2   ∪ 3 , ∞ .

Resposta

f o g = f g x = x - 2 x - 3

A função é contínua no intervalo: - ∞ , 2   ∪ 3 , ∞

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em que pontos a função abaixo é contínua? y = xt gx x 2 + 1
Em que pontos as funções deixam de ser contínuas? Em que pontos, se houver, as descontinuidades são removíveis? E não removíveis? Justifique suas respostas.
Em que pontos a função abaixo é contínua? y = t g πx 2
Em que pontos a função abaixo é contínua? y = cos ⁡ x x
Em que pontos a função abaixo é contínua? y = 1 x + 2 2 + 4