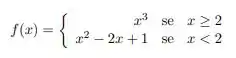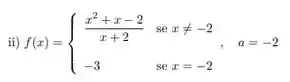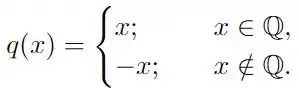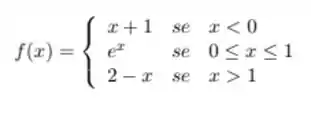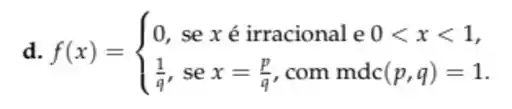Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios de Continuidade - Lista de Exercícios Resolvida

Ver Teoria

Questão 1

Calcule a constante A para que a função abaixo seja contínua:

f x = sen ⁡ 1 x - x + x ,       x < 0 cos ⁡ x - A ,       x ≥ 0

Ver solução completa

Questão 2

Verifique se a função é contínua no ponto indicado. Justifique a resposta.

f t = 1 - t 1 - t 3                       s e     t ≠ 1 3 / 2                                       s e   t = 1

Ver solução completa

Questão 3

Considere

f x = a 2 sen ⁡ 4 x x   s e x < 0 b s e x = 0 b 2 + 1 - cos ⁡ x x sen ⁡ 1 x s e x > 0

Determine os pares ordenados a , b de forma que essa função seja contínua em x = 0 .

Ver solução completa

Questão 4

Calcule o valor das constantes a e b para que a função abaixo seja contínua em x = 0 .

f ( x ) = 1 x + 2 ,       s e   x < 0 a ,       s e   x = 0 sen ⁡ ( b x ) x ,       s e   x > 0

Ver solução completa

Questão 5

Determine as constantes A e B para que a função abaixo seja contínua em x 0 = 2 .

f x = x 3 - x 2 + x - 1 ,     x > 2 A ,     x = 2 B - x 2 ,     x < 2

Ver solução completa

Questão 6

Sabe-se que f é contínua em 2 e que f ( 2 ) = 8 . Mostre que existe δ > 0 tal que para todo x ∈ D f

2 - δ < x < 2 + δ → f ( x ) > 7 .

Ver solução completa

Questão 7

Seja f uma função definida em ℝ e suponha que existe M > 0 tal que | f ( x ) - f ( p ) | ≤ M | x - p | para todo x . Prove que f é contínua em p .

Ver solução completa

Questão 8

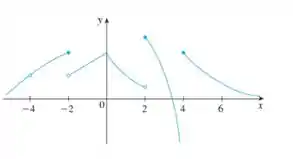
Considere a função f definida pelo gráfico abaixo.

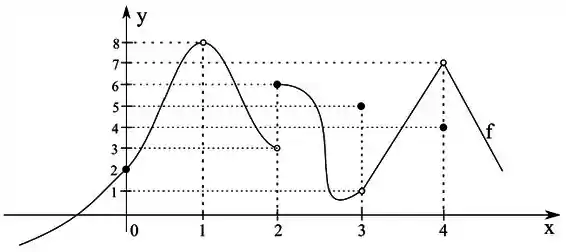
  1. Determine o lim x → a ⁡ f x para a = 0,1 , 2,3 , 4 se existir
  2. Em que ponto f não é contínua

Ver solução completa

Questão 9

Considere f definida por:

f x = x 2 - 9 x + 3 s e   x > - 3 4 s e   x = - 3 x 2 + a s e   x < - 3

  1. Determine a tal que lim x → - 3 - ⁡ f x = f - 3
  2. Para o valor de a calculado no item anterior, f é contínua em x = - 3 ?
  3. Calcule lim n → ∞ ⁡ f - 3 + 1 n , se existir

Ver solução completa

Questão 10

11 – Considere a função

f x = x + 1 ,     s e   x ≤ 0 c x ,     s e   x > 0

a) Existe uma constante c para qual a constante seja contínua em x = 0 ? Justifique sua resposta.

b) se existir uma constante c tal que f x seja contínua em x = 0 , esboce o gráfico de f x .

Ver solução completa

Questão 11

Verifique se a função dada é contínua no ponto x = 1 .

f x = x - 1 x - 1       x ≠ 1 2                                   x = 1

Ver solução completa

Questão 12

1) Sejam a e b números reais tais que a função

f x = sin ⁡ ( 24 x ) x ,   s e   x < 0 x 2 + a x + b ,   s e 0 ≤ x ≤ 6 18 ,   s e   x > 6

É continua em toda parte. O valor de f ( 1 ) é

Escolha uma:

a) 18

b) 22

c) 16

d) 20

e) 14

Ver solução completa

Questão 13

Seja

f x = x + 1 ,     s e   x ≥ 1 2 x ,                     s e   x < 1

( a ) A função é contínua em x = 1 ? Justifique sua resposta.

Ver solução completa

Questão 14

  1. Explique o que significa dizer que uma função f é contínua no ponto x = a .

.

Ver solução completa

Questão 15

Considere a função f ( x , y ) dada pela expressão

f x , y = { - 3 x y 2 - x 3 x 2 + y 2 ,     x , y ≠ ( 0,0 )   1 ,     x , y = ( 0,0 )  

  1. Se ( x 0 , y 0 ) ≠ ( 0,0 ) , explique se f é ou não contínua em x 0 , y 0 ). Em seguida, calcule

    2. f ( x , y )  

  2. Explique se f é ou não contínua em 0,0 .

Ver solução completa

Questão 16

Questão 2 - Seja f : R → R , definida por

f x = s e n a x 5 x - 1 , s e   x < 0 x 2 - 4 x + 3 x - 1 , s e   0 ≤ x < 1 b , s e   x = 1 x c x - 1 s e   x > 1

Determine o valor das constantes reais a , b e c que tornam f contínua em todo R .

Ver solução completa

Questão 17

Seja f x = x 2 - 3 x 3 sen ⁡ 1 x - 3 3 + arctg ⁡ x ,     s e   x ≠ 3 1 ,                                                         s e   x = 3

a ) Determine todos os pontos em que f não é contínua. Justifique.

b ) Determine todos os pontos em que f não é derivável. Justifique.

c ) Calcule a derivada de f nos pontos em que f é derivável.

Ver solução completa

Questão 18

4) Determine os valores das constantes A e B , de tal forma que a função f definida por:

f x = 3 x , s e x ≤ 2 A x + B , s e 2 < x < 5 - 6 x , s e x ≥ 5

Seja continua no intervalo - ∞ , ∞ .

Ver solução completa

Questão 19

Verifique se a função dada é contínua no ponto x = 1 .

f x = x - 1 x - 1   p a r a   x ≠ 1 2   p a r a   x = 1

Ver solução completa

Questão 20

Verifique se a função dada é contínua nos pontos indicados. Justifique a resposta.

f x = 1 2 x - 1 x ,     - 2 ≤ x ≤ 2

Onde x   é a função maior inteiro que não supera x . Nos pontos x = 0 e x = 1

Sugestão: Esboce o gráfico de f

Ver solução completa

Questão 21

Seja f definida por

f x = x 3 + 2 x 2 + x x 3 + 5 x 2 + 7 x + 3 s e x ≠ - 3 , x ≠ - 1 0 s e x = - 3 - 1 2 s e x = - 1

a) A função f está definida em R ? Justifique

b) Dê os pontos onde f é contínua. Justifique

c) Dê os pontos f é descontínua. Justifique

d) A função f é contínua em R ? Justifique

Ver solução completa

Questão 22

Verifique a continuidade das funções abaixo no ponto 0,0 .

c) g x , y =   x 2 y x 2 + y 2 ,           s e   x , y ≠ ( 0,0 ) 0 ,                           s e   x , y = ( 0,0 )

Ver solução completa

Questão 23

Resolva os itens abaixo justificando detalhadamente suas soluções.

( a ) A função definida por f x = x 2 - 1 x - 1 para x ≠ 1 e f 1 = 2 é contínua em x = 1 ?

Ver solução completa

Questão 24

Verifique a continuidade das funções abaixo no ponto 0,0 .

a) f x , y =   - 2 x y + 1 x 2 + y + 1 4 ,             s e   x , y ≠ ( 0 , - 1 ) 0 ,                                         s e   x , y = 0 , - 1

Ver solução completa

Questão 25

Considere as afirmativas abaixo:

  1. Se h é descontínua no ponto x = c , então o limite lateral em lim x → c + ⁡ h ( x ) não existe.
  2. Se lim x → 1 ⁡ ( g x + f ( x ) ) existe, então lim x → 1 ⁡ f ( x ) existe.

É verdadeira ou são verdadeiras:

  1. Nenhuma das afirmativas.
  2. Somente a afirmativa (II).
  3. Somente a afirmativa (I).
  4. As afirmativas (I) e (II).

Ver solução completa

Questão 26

(b) Ache os pontos dos parâmetros A e B para que a função seja continua em x = 1   , onde f é definida por

f x =   x - 1 2 sen ⁡ 1 x - 1 + A ,       s e   x > 1 2                                                         ,         s e   x = 1 x 2 - B + 1 x + B x - 1 ,     s e   x < 1

Ver solução completa

Questão 27

Para que a função f : R → R seja contínua em R , o valor de m n deve ser:

f x = 3 x 2 - 7 x + 2 ,   s e   x > 1 m x + n ,   s e - 1 ≤ x ≤ 1 s e n π x 2 ,   s e   x < - 1

Ver solução completa

Questão 28

Para que a função

f x = x 2 + 2 x - 3 x - 1 ,                     s e   x < 1 x + k ,                                                     s e   x ≥ 1

Seja contínua em R o valor da constante k deve ser

Ver solução completa

Questão 29

Seja

f x , y = y 3 x 2 + y 2 ,               x ,   y ≠ ( 0,0 ) 0 ,                                         x , y = ( 0,0 )

  1. Determine se f é contínua no ponto ( 0,0 ).
  2. Determine se f é diferenciável no ponto (0,0).

Ver solução completa

Questão 30

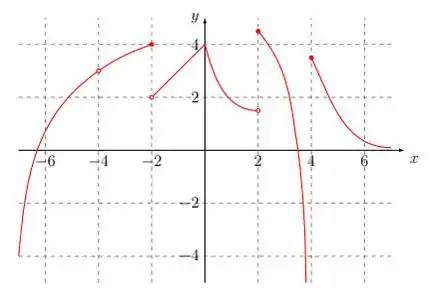
  1. Considere a função f cujo gráfico está representado abaixo. Determine os pontos de continuidade e descontinuidade de f .

Ver solução completa

Questão 31

  1. Em cada item, use as propriedades de continuidade para explicar por que a função é contínua em seu domínio.
  1. f x = arcsin ⁡ x 2 - 1
  2. f x = 6 + sin ⁡ ( x + sin ⁡ x ) x 2

Ver solução completa

Questão 32

Determine se as seguintes funções são contínuas em D ( f ) :

  1. f x = x 2 - 9 x - 3  

Ver solução completa

Questão 33

Determine se as seguintes funções são contínuas em D ( f ) :

b )   g x = x 2 - 9 x - 3 ,     s e   x ≠ 3 3 ,     s e   x = 3  

Ver solução completa

Questão 34

Defina a função f : R ⟶ R por

f x =   3 a x + x - 2 3 cos ⁡ x 2 - 4 x - 2   s e   x < 2 , 12 π                                                                                                 s e   x = 2 , b s e n π x 2 - 4 π x - 2                                             s e   x > 2 .

Sabendo que f é contínua em x = 2 é correto afirmar que o valor do produto a ⋅ b é:

  1. 12 π
  2. 8 π
  3. 6 π
  4. 2 π
  5. π
  6. 4 π
  7. 3 π
  8. 0

Não é necessário justificativa.

Ver solução completa

Questão 35

Discuta a continuidade de f :

d) f x ,   y = x y x + y     s e   x ,   y ≠ ( 0 ,   0 ) 0 ,     s e   x ,   y = ( 0 ,   0 )

Ver solução completa

Questão 36

Discuta a continuidade de f :

a) f x ,   y = x y x 2 + y 2     s e   x ,   y ≠ ( 0 ,   0 ) 0 ,     s e   x ,   y = ( 0 ,   0 )

Ver solução completa

Questão 37

Discuta a continuidade de f :

b) f x ,   y = x 2 y x 4 + y 2     s e   x ,   y ≠ ( 0 ,   0 ) 0 ,     s e   x ,   y = ( 0 ,   0 )

Ver solução completa

Questão 38

Discuta a continuidade de f :

c) f x ,   y = x + y x 2 + y 2     s e   x ,   y ≠ ( 0 ,   0 ) 0 ,     s e   x ,   y = ( 0 ,   0 )

Ver solução completa

Questão 39

Determine a região de continuidade de f e trace o esboço, mostrando com uma região sombreada em R 2 a região de continuidade de f :

c) f x ,   y = x y 16 - x 2 - y 2

Ver solução completa

Questão 40

Determine a região de continuidade de f e trace o esboço, mostrando com uma região sombreada em R 2 a região de continuidade de f :

d) f x ,   y = x 4 x 2 - 9 y 2 - 36

Ver solução completa

Questão 41

Mostre que a função é descontínua na origem. Depois determine se a continuidade é removível ou essencial. Se a descontinuidade for removível defina f ( 0 ,   0 ) tal que remova a descontinuidade.

b) f x ,   y = x + y sin ⁡ x y

Ver solução completa

Questão 42

Mostre que a função é descontínua na origem. Depois determine se a continuidade é removível ou essencial. Se a descontinuidade for removível defina f ( 0 ,   0 ) tal que remova a descontinuidade.

c) f x ,   y = x 2 y 2 x 2 + y 2

Ver solução completa

Questão 43

Mostre que a função é descontínua na origem. Depois determine se a continuidade é removível ou essencial. Se a descontinuidade for removível defina f ( 0 ,   0 ) tal que remova a descontinuidade.

d) f x ,   y = x 3 y 2 x 6 + y 4

Ver solução completa

Questão 44

Mostre que a função é descontínua na origem. Depois determine se a continuidade é removível ou essencial. Se a descontinuidade for removível defina f ( 0 ,   0 ) tal que remova a descontinuidade.

a) f x ,   y = x y x + y

Ver solução completa

Questão 45

Dada a função f definida por

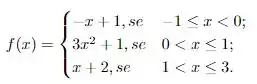
Estude a continuidade de f em x = 1 . Defina f em x = 0 de modo a tornar f contínua neste ponto.

Ver solução completa

Questão 46

Considere a função

f x = x e x 3 ,             x ≥ 1 a x 2 ,                 x < 1

Encontre o valor de a para que f seja contínua em x = 1 .

Ver solução completa

Questão 47

( b ) Verifique se a função

f x = x 2 - 2 x + 1 x 2 - 3 x + 2 + 2 x - 1 cos ⁡ x - 1 ,                       s e   x ≠ 1 1 ,                                                                                                                                                         s e   x = 1

É contínua em x = 1 . Justifique.

Ver solução completa

Questão 48

4. Considere a função f dada por

f x = e x 2 + 1 sin ⁡ π x - ln ⁡ x 2 + e cos ⁡ π x

  1. Mostre que f é continua para todo x real.
  2. Mostre que f tem pelo menos uma raiz real.

Ver solução completa

Questão 49

Calcule os seguintes limites (não é permitido o uso da regra de l’Hôspital):

c lim x → 0 ⁡ f x , onde

f x = sen ⁡ x x + sen ⁡ x ,       s e   x ≠ 0 0 ,       s e   x = 0

A função f é contínua em x = 0 ? (Justifique!)

Ver solução completa

Questão 50

Mostre que existe um número real que é igual a soma de seu cubo e de seu quadrado menos cinco.

Ver solução completa

Questão 51

4. Use a continuidade das funções do exercício anterior para calcular os limites abaixo:

  1. lim x → 1 ⁡ x 2 - 3 x + 4 e x
  2. lim x → 0 - ⁡ 2 sin ⁡ x - x 2 - 9 x - 3 ⁡

Ver solução completa

Questão 52

2. Use a continuidade das funções do exercício anterior para calcular os limites abaixo:

  1. lim x → 1 2 ⁡ arcsin ⁡ ( x 2 - 1 )
  2. lim x → π ⁡ 6 + sin ⁡ ( x + sin ⁡ x ) x 2 ⁡

Ver solução completa

Questão 53

Verifique se a função f abaixo é contínua no ponto a indicado

x 2 - 8 ,   s e   x < 3

s i n ( x - 3 ) x - 3   s e   x > 3

1   s e   x = 3

onde a = 3

Ver solução completa

Questão 54

Verifique se a função f abaixo é contínua no ponto a indicado

x - x 2 ,   s e   x < - 2

x 3 + 2   s e   x > - 2

3   s e   x = - 2

onde a = 3

Ver solução completa

Questão 55

Determine o valor de L para que as funções abaixo sejam contínuas.

c )   f x = x - 5 x + 5 - 10 , s e     x ≠ 5 L , s e       x = 5

Ver solução completa

Questão 56

Verifique se a função abaixo é contínua no ponto a indicado

x + 3 ,   s e   x ≤ 1

4   s e   x > 1

onde a = 1

Ver solução completa

Questão 57

Determine os valores de a   e   b para que a função seja contínua para qualquer x .

a )   f x = x 2 - 1 ,   s e     x < 3 2 a x   , s e       x ≥ 3

Ver solução completa

Questão 58

Determine os valores de a   e   b para que a função seja contínua para qualquer x .

e )   f x = a x + 2 b ,   s e     x ≤ 0 x 2 + 3 a - b   , s e       0 < x ≤ 2 3 x - 5 ,   s e   x > 2

Ver solução completa

Questão 59

Determine os valores de a   e   b para que a função seja contínua para qualquer x .

c )   f x = a 2 x - 2 a ,   s e     x ≥ 2 12   , s e       x < 2

Ver solução completa

Questão 60

Determine os valores de a   e   b para que a função seja contínua para qualquer x .

d )   f x = - 2 ,   s e     x ≤ - 1 a x - b   , s e       - 1 < x < 1 3 ,   s e   x ≥ 1

Ver solução completa

Questão 61

Considere a função

f x = x ²   -   3 x   +   2 x - 1

Mostre que lim x → 1 ⁡ f ( x ) existe. A função   f   é contínua em x   =   1 ?

Ver solução completa

Questão 62

  1. Determine os possíveis valores de a , b e c que tornam continuas as funções abaixo e esboce seus gráficos.

f x = x 2 - 4 x - 2 ,   s e   x < 2 a x 2 - b x + 3 ,   s e   2 ≤ x < 3 2 x - a + b ,   s e   x ≥ 3

Ver solução completa

Questão 63

  1. Determine os possíveis valores de a , b e c que tornam contínuas as funções abaixo e esboce seus gráficos.
  1. f x = a x 2 + 2 x ,   s e   x < 2 x 3 - a x ,   s e   x ≥ 2

Ver solução completa

Questão 64

Verifique se a função dada é contínua no ponto x = 1 .

f x = x - 1 x - 1       x ≠ 1 2                                   x = 1

Ver solução completa

Questão 65

Verifique se a função dada é contínua nos pontos indicados.

f x = x 2 + 1 x 6 + x 2 + 2

Em qualquer x ∈ R .

Ver solução completa

Questão 66

Verifique se existe a   ϵ   R tal que

f x = 1 + a x ,         x ≤ 0 x 4 + 2 a ,       x > 0

seja contínua em R

Ver solução completa

Questão 67

Questão 3: Seja f : R → R dada por

f x = - 6 x - 3 x - 2                 ,         s e       x ≥ 1   4 x - 1                           ,         s e       x < 1                

  1. A função é contínua em x = 1 ? Justifique sua resposta.

Ver solução completa

Questão 68

Questão 1:

  1. Calcule o seguinte limite:

    2. lim x → 0 ⁡ x 2 + 9 - x + 9 5 x

  2. Seja a um número diferente de z e r o . Calcule o seguinte limite:

    3. lim x → 0 ⁡ sen ⁡ 3 x a x

  3. Determine valores de a , b de modo a que a função f seja contínua em x = 0 , onde

f x = x 2 + 9 - x + 9 5 x             s e           x > 0 sen ⁡ 3 x a x                                                   s e           x < 0 b                                                                             s e           x = 0

Ver solução completa

Questão 69

Questão 2:

Para quais valores de c a função abaixo é contínua em - ∞ ,   ∞ ?

f x = c 2 x 2 + 2 x                       s e                       x < 2 x 3 - c x                                 s e                       x ≥ 2

Ver solução completa

Questão 70

Determine o valor de L para que as funções abaixo sejam contínuas.

b )   f x = x - 3 x - 3 , s e     x ≠ 3 L , s e       x = 3

Ver solução completa

Questão 71

Considere a seguinte função f : I R - I R dada por:

f x = x 2 - 3 x + 2 b x 2 - 1 ,     x < 1 sin ⁡ x 2 - 1 x - 1 ,     x > 1 c ,     x = 1

Os valores reais de b ≠ 0 e c que tornam f contínua são:

  1. b = - 1 4 e c = 2
  2. b = - 1 2 e c = 2
  3. b = - 1 3 e c = 2
  4. b = - 1 2 e c = 1
  5. b = - 1 4 e c = 1

Ver solução completa

Questão 72

Considere a função f : - π , π → I R definida por

f x = 1 - cos ⁡ x s i n ²   x   ,     s e   x ≠ 0 β ,     s e   x = 0

O valor de β para que f seja contínua em x = 0 é:

  1. 2
  2. 1 2
  3. 2 3
  4. 1 4

Ver solução completa

Questão 73

Q01II) Considere a função abaixo

f x = - a x + 3 ,     s e   0 < x ≤ 2 x - b ,     s e   2 < x ≤ 3 2 ,     s e   3 < x ≤ 4

Encontre valores de a e b de modo que f seja uma função contínua.

Ver solução completa

Questão 74

2) Considere a função f definida como:

f x = 3 x - 1 - 3 x + 1 x ,     p a r a   x > 0 a ,     p a r a   x = 0 sin ⁡ a x x ,     p a r a   x < 0

Determine o valor de a para que tenhamos f contínua em I R

Ver solução completa

Questão 75

Considere a função f : I R → I R definida por:

f x = a ,     s e   x = 0 sin ⁡ x x - 2 3 x ,     s e   x ≠ 0

(a) Determine o valor de a ∈ I R para que f seja contínua em x = 0

Ver solução completa

Questão 76

Seja f : I R → I R uma função e suponha que para todo x ≠ 0 tenhamos

cos ⁡ x - 1 ≤ f x ≤ x 4 + x 2                     1

(a) Calcule o limite lim x → 0 ⁡ f x

(b) Mostre que se f for contínua então f 0 = 0

(c) Dê um exemplo de uma função contínua satisfazendo 1

Ver solução completa

Questão 77

Determine a região de continuidade de f e trace o esboço, mostrando com uma região sombreada em R 2 a região de continuidade de f :

a) f x ,   y = y x 2 - y 2 - 4

Ver solução completa

Questão 78

Determine a região de continuidade de f e trace o esboço, mostrando com uma região sombreada em R 2 a região de continuidade de f :

b) f x ,   y = x 2 + y 2 9 - x 2 - y 2

Ver solução completa

Questão 79

14) Verifique se a função dada é contínua nos pontos indicados. Justifique a resposta.

f x = 1 2 x - 1 [ x ] para - 2 ≤ x ≤ 2 , onde [ x ] = maior inteiro que não supera x . Pontos x = 0 e x = 1.(Sugestão: esboce o gráfico de f )

Ver solução completa

Questão 80

13) Verifique se a função dada é contínua nos pontos indicados. Justifique a resposta.

f x = x 2 + 1   x 6 + x 2 + 2 em qualquer x ∈ R

Ver solução completa

Questão 81

Seja a um número real não nulo tal que a função f definida por

f x = x 2 + 6 a x + a 2 ,       s e   x ≤ 5 11 x + 34 a - 30 ,       s e   x > 5

É contínua em todo domínio. O valor de f ( - 1 ) é

Escolha uma:

a ) - 5

b ) - 9

c ) - 7

d ) - 13

e ) - 17

Ver solução completa

Questão 82

Sejam a e b tal que a função

f x = - 9 ,       s e   x ≤ - 15 ,                                 a x + b ,         s e - 15 < x ≤ 0 6 - x 2 ,       s e   x > 0                                

É contínua em todo ponto. O valor de 3 f ( - 5 ) é

Escolha uma:

a )   3

b )   51

c ) - 7

d )   21

e )   39

Ver solução completa

Questão 83

Encontre os valores de a e b que tornam f continua em toda parte.

f x =   { x 2 - 4 x - 2 ,     s e   x < 2                                 a x 2 - b x + 3 ,       s e   2 < x < 3   2 x - a + b ,       s e   x ≥ 3                            

Calcule 2 a + b

Ver solução completa

Questão 84

Considere a função

f x = a x + b ,   x < 1 x 2 + 1 , x ≥ 1

  1. Calcule o limite lim h → 0 + ⁡ f 1 + h - f 1 h
  2. Determine as constantes a e b para que f seja derivável em x = 1

Ver solução completa

Questão 85

Verifique a continuidade das funções abaixo no ponto 0,0 .

d) h x , y =   x y 2 x 2 + y 4 ,               s e   x , y ≠ ( 0,0 ) 0 ,                             s e   x , y = ( 0,0 )

Ver solução completa

Questão 86

Considere uma função contínua f : [ 0,1 ] ⟶ R tal que 0 < f ( x ) < 1 para todo 0 ≤ x ≤ 1 .

  1. Defina g : [ 0,1 ] ⟶ R por g x = f x - x . Mostre que g é contínua.
  2. Use a função g para mostrar que existe um ponto c   ϵ   0,1 tal que f c = c .

Ver solução completa

Questão 87

  1. Determine, caso possível, as constantes a ,   b ∈ R tais que f ( x ) seja contínua em x = 0 .

    2. f x = x + a 2 - 4 a - arctan ⁡ 11 x ,       x < 0 a - 1 ,                                         x = 0 sin ⁡ b x ln ⁡ 1 + 100 x ,       x > 0

  2. Encontre a equação da reta normal à curva y = 2 x - 3 e paralela à reta 9 x + 3 y - 5 = 0

Ver solução completa

Questão 88

Um atacadista deseja cobrar R $ 2,00 por cada metro de tecido até 10 metros e R $ 1,50 por cada metro a partir de 10 metros. Para tanto, ele estipulou o preço P ( x ) de x metros por

P x = 2 x ,       0 ≤ x ≤ 10 1,5 x ,       10 < x

  1. Quanto se paga por 9 e por 12 metros? Explique por que a função acima não reflete o desejo do atacadista.
  2. Alterando a segunda linha para P x = 1,5 x + A , 10 < x , use a definição de continuidade para determinar a constante A de modo que a função satisfaça o desejo do atacadista. Quais os preços de 9 e 12 metros, usando a função modificada?

Ver solução completa

Questão 89

Verifique se a função f abaixo é contínua no ponto a indicado

1 - x 2 ,   s e   x < 2

x - 5   s e   x > 2

0   s e   x = 2

onde a = 2

Ver solução completa

Questão 90

Verifique se a função f abaixo é contínua no ponto a indicado

s i n ( x ) x ,   s e   x < 0

t g ( x ) x   s e   x > 0

1   s e   x = 0

onde a = 0

Ver solução completa

Questão 91

Qual deve ser o valor de L para que função f abaixo seja contínua?

x 3 - 8 x - 2 ,   s e   x ≠ 2

L     s e   x = 2

Ver solução completa

Questão 92

Considere a função f : ℝ → ℝ dada por

b) Calcule os seguintes limites, justificando suas respostas:

l i m x → 3 - f ( x )

Ver solução completa

Questão 93

Considere a função f : ℝ → ℝ   dada por

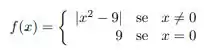
b) Calcule os seguintes limites, justificando suas respostas:

l i m x → 0 f ( x )

Ver solução completa

Questão 94

Considere a função f : ℝ → ℝ dada por

Ver solução completa

Questão 95

6. Considere a função

f x = 2 x 3 - 2 3 x 2 - 3 ,   s e   x < 1 α ,   s e   x = 1 β x 2 - 1 x - 1 ,   s e   1 < x < 2 γ x 2 + 1 2 x ,   s e   x ≥ 2

Encontre valores reais para α , β e γ tais que a função f seja continua nos pontos x 0 = 1 e x 0 = 2 .

Ver solução completa

Questão 96

Determine os valores de a   e   b para que a função seja contínua para qualquer x .

b )   f x = x ,   s e     x < - 2 b x ²   , s e       x ≥ - 2

Ver solução completa

Questão 97

Esboce o gráfico da função

f x = 1 ,   s e   x ≤ - 1 - x ,   s e - 1 < x < 0 1 ,   s e   x = 0 - x ,   s e   0 < x < 1 1 ,   s e   x ≥ 1

Discuta, em detalhes, limites laterais, continuidade e continuidade lateral de f quando x = - 1 ,   0   e - 1 . Alguma da descontinuidade pode ser removida?

Ver solução completa

Questão 98

Considere a função f : ℝ → ℝ dada por

a) Construa o gráfico de f .

Ver solução completa

Questão 99

Considere a função f : ℝ → ℝ dada por

b) Calcule os seguintes limites, justificando suas respostas:

l i m x → 3 + f ( x )

Ver solução completa

Questão 100

Esboce os gráficos e verifique se as seguintes funções são contínuas em cada um dos seus respectivos domínios. Justifique suas respostas:

  1. f : ℝ → ℝ dada por

f ( x )   =   x

Ver solução completa

Questão 101

Esboce os gráficos e verifique se as seguintes funções são contínuas em cada um dos pontos de

seus respectivos domínios. Justifique suas respostas:

e) f : ℝ → ℝ dada por:

Ver solução completa

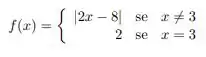
Questão 102

Esboce os gráficos e verifique se as seguintes funções são contínuas em cada um dos seus respectivos domínios. Justifique suas respostas:

d) f : ℝ → ℝ dada por

Ver solução completa

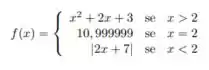
Questão 103

Esboce os gráficos e verifique se as seguintes funções são contínuas em cada um dos seus respectivos domínios. Justifique suas respostas:

b) f : R → R dada por

Ver solução completa

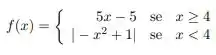
Questão 104

Esboce os gráficos e verifique se as seguintes funções são contínuas em cada um dos seus respectivos domínios. Justifique suas respostas:

c) f : ℝ → ℝ dada por

Ver solução completa

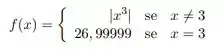
Questão 105

3. Seja f :   R → R uma função contínua tal que f 0 = f 2 e defina g :   R → R por g x = f x - f x - 1

  1. Mostre que g é continua
  2. Mostre que g 1 + g 2 = 0
  3. Mostre que existe a ∈ [ 1,2 ] tal que f a = f a - 1

Ver solução completa

Questão 106

Esboce os gráficos e verifique se as seguintes funções são contínuas em cada um dos pontos de

seus respectivos domínios. Justifique suas respostas:

f) f : ℝ → ℝ dada por:

Ver solução completa

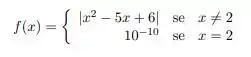
Questão 107

2. Calcule o valor de a , b ∈ R , com a > 0 e b ≠ 0 considere a função

f x = 5 x - π 2 + a 2 - 5 a b x - π 2 ,   s e   x < π 1                                         ,   s e   x = π b - 1 sin ⁡ a x - π x - π   ,   s e   x > π

Determine os valores de a e b para que f seja continua em x = π .

Ver solução completa

Questão 108

Considere a função f :   R ⟶ R definida por

f x = x 3 + x - 2 s e n 1 x - 2     s e   x < 2 ,   a                                                                                             s e   x = 2 , b x 2 - 4 x - 2                                                         s e   2 < x .

Encontre valores reais para a e b tais que a função f seja contínua em todos os pontos do seu domínio. Justifique a resposta.

Ver solução completa

Questão 109

4. Defina a função f :   R →   R por

f x = 2 a x + x - 2 3 cos ⁡ x 2 - 4 x - 2     s e   x < 2 12 π                                                                                                     s e   x = 2 b sin ⁡ π x - 2 π x - 2                                                         s e   x > 2

Sabendo que f é contínua em x = 2 , é correto afirmar que o valor do produto a b é:

  12 π       24 π       6 π       9 π       36 π       4 π       3 π       2 π

Ver solução completa

Questão 110

Seja f : R ⟶ R uma função contínua tal que f 0 = f ( 2 ) e defina g : R ⟶ R   por g x = f x - f ( x - 1 ) . Considere as afirmações:

  • g não é contínua
  • g 1 + g 2 = 0
  • Existe a   ϵ   1,2 tal que f a = f a - 1
  • lim x ⟶ 0 ⁡ g e 4 x + g t g 2 x x = 0
  • g 1 = f 1 - f ( 2 )
  • Se f x = x ( x - 2 ) então g x = 2 x + 3

Então o número exato de afirmações incorretas é:

  1. 0
  2. 1
  3. 2
  4. 3
  5. 4
  6. 5
  7. 6

Não é necessário justificativa.

Ver solução completa

Questão 111

Verifique se a função é contínua no ponto indicado. Justifique a resposta.

f x = 1 - t 1 - t 3 ,       s e   t ≠ 1 3 2 ,     s e   t = 1 em t = 1

Ver solução completa

Questão 112

Considere a função f : ℝ → ℝ   dada por

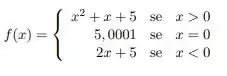
b) Calcule os seguintes limites, justificando suas respostas:

l i m x → 0 f ( x )

Ver solução completa

Questão 113

a Considere f contínua definida por:

f x = x 2 - 2 x - 24 x - 6 s e x < 6 a s e x = 6 x 11 - 216 x 8 - 1295 x 7 + 279720 x 4 - 1286 x 3 + 277776 x 3 - 216 s e x > 6

Determine lim x → 6 ⁡ f ( x ) . Qual o valor de a ?

Ver solução completa

Questão 114

Considere a função

f x = e x + 1 ,                                                 x ≤ - 1 x 2 ,                                     - 1 < x < 1 1 + ln ⁡ x ,                                     x ≥ 1

( a ) Determine os pontos de continuidade de f

Ver solução completa

Questão 115

Para a função f   definida por f x = - 2 - x , x < 1 a x + b , 1 ≤ x < 2 x 2 - 7 x + 12 , x ≥ 2

a) Determine os valores de a e b   para que f seja contínua em R .

b) Esboce o gráfico de f .

Ver solução completa

Questão 116

29. Prove pela definição, que a função dada é contínua no ponto dado.

a) f x = 4 x - 3 em p = 2

Ver solução completa

Questão 117

29. Prove pela definição, que a função dada é contínua no ponto dado.

c) f x = - 3 x em p = 1

Ver solução completa

Questão 118

29. Prove pela definição, que a função dada é contínua no ponto dado.

d) f x = x 3 em p = 2

Ver solução completa

Questão 119

Encontre os valores de a e b , se possível, tais que a função

f x = x 2 + x - 1 , s e   x < 1 a x + b , s e   1 ≤ x ≤ 2 x 2 - 2 , s e   x > 2 ,

seja contínua para todo x . Justifique.

Ver solução completa

Questão 120

Verifique se a função é contínua no ponto indicado. Justifique a resposta.

f x = x ³ cos ⁡ 1 x ,       s e   x ≠ 0 1 ,     s e   x = 0 em x = 0

Ver solução completa

Questão 121

Seja

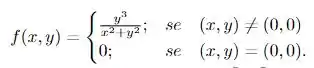
responda justificando.

( a ) f ( x , y ) é contínua em ( 0,0 ) ?

( b ) f ( x , y ) possui derivadas parciais em ( 0,0 ) ? Caso afirmativo calcule-as.

( c ) f ( x , y ) é diferenciável em ( 0,0 ) ?

Ver solução completa

Questão 122

Determine os valores de a   e   b que tornam a função abaixo contínua em toda parte

Ver solução completa

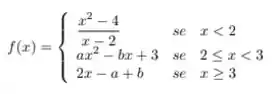
Questão 123

Seja f a função definida por

f x = - 3 ,     s e   x < - 1 x 2 + 1 ,     s e - 1 ≤ x < 0 ( x + 1 ) ( x - 2 ) x - 2 ,     s e   0 ≤ x < 3 4 ,       s e   x ≥ 3

d) f é contínua no intervalo fechado - 1 2 , 1 ? Justifique.

Ver solução completa

Questão 124

Encontre valores apropriados para m e b de modo que a função

f x = x 2 ,     x < 1 m x + b ,     x ≥ 1

seja derivável em 1 e faça um esboço do gráfico de f .

Ver solução completa

Questão 125

Considere

f x = x 2 + 2 ,     x < 1 2 x + 1 ,     x ≥ 1

Sem fazer cálculos é possível afirmar que f é contínua em 1 ?

Ver solução completa

Questão 126

Considere

f x = x sin ⁡ 1 x ,     x ≠ 0 0 ,     x = 0

Verifique se f é contínua em 0 .

Ver solução completa

Questão 127

Considere a função f : ℝ → ℝ   dada por

  1. Construa o gráfico de f ;

Ver solução completa

Questão 128

Considere a função f : ℝ → ℝ   dada por

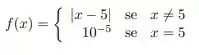
b) Calcule os seguintes limites, justificando suas respostas:

l i m x → 5 f ( x )

Ver solução completa

Questão 129

Considere

f x = x 2 + 2 ,     x < 1 2 x + 1 ,     x ≥ 1

Verifique se f é derivável em 1 .

Ver solução completa

Questão 130

Considere a função f : ℝ → ℝ dada por

b) Calcule os seguintes limites, justificando suas respostas:

l i m x → 3 f ( x )

Ver solução completa

Questão 131

Considere a função f : ℝ → ℝ   dada por

  1. Construa o gráfico de f ;

Ver solução completa

Questão 132

Considere

f x = x sin ⁡ 1 x ,     x ≠ 0 0 ,     x = 0

Verifique se f é derivável em 0 .

Ver solução completa

Questão 133

Determine a equação da reta tangente ao gráfico da função f dada passando pelo ponto a ,   f a , caso elas existam.

(a) f x = x 2 + 2 x + 5 e a = 1

Ver solução completa

Questão 134

Calcule (atenção: não é permitido usar derivadas no cálculo dos limites):

d)

d d x e 2 x ln ⁡ x + x tan ⁡ x

Ver solução completa

Questão 135

Seja

f x = x sin ⁡ ( π x ) ,     x ≤ 2 x 2 + 1 cos ⁡ π x ,     x > 2

Verifique se f é contínua e diferenciável em x = 2 .

Ver solução completa

Questão 136

Determine L para que a função f definida abaixo seja contínua em x = 0 .

f x = x 4 cos ⁡ 1 x ,   s e   x ≠ 0 L ,   s e   x = 0

Ver solução completa

Questão 137

Determine a e b sabendo que a função

f x = x 2 - a x + 4 x + 4   s e   x < - 4 - x + b   s e   x ≥ - 4

é contínua.

Ver solução completa

Questão 138

1. Quais das funções abaixo são contínuas em x 0 = 3 ? Justifique.

a) f x = x 2 - 5 x + 6 x - 3

Ver solução completa

Questão 139

1. Quais das funções abaixo são contínuas em x 0 = 3 ? Justifique.

c) h x = x 2 - 9 x - 3 ,     s e   x ≠ 3 6 ,     s e   x = 3

Ver solução completa

Questão 140

1. Quais das funções abaixo são contínuas em x 0 = 3 ? Justifique.

d) k x = x 2 - 9 x - 3 ,     s e   x < 3 x 2 - 2 x + 3 ,     s e   x ≥ 3

Ver solução completa

Questão 141

Diga se cada afirmativa abaixo é verdadeira ou falsa, justificando sua resposta:

  1. A função

f x = 1 - x 2 ,   x < - 1 ln ⁡ 2 - x 2 ,   - 1 ≤ x ≤ 1 x - 1 x + 1 ,   x > 1

É contínua ∀ x ∈ R .

Ver solução completa

Questão 142

Calcule os valores possíveis para c para que a função

f x = 1 - x 1 - x 3 ,     x ≠ 1 c 2 ,     x = 1

Seja contínua ∀ x ∈ R .

Ver solução completa

Questão 143

Defina se f é contínua em a

Ver solução completa

Questão 144

De o domínio da função

f ( x   ) = e x ² + 9 + x 5

Ver solução completa

Questão 145

1. Quais das funções abaixo são contínuas em x 0 = 3 ? Justifique.

b) g x = x 2 - 3 x x - 3 ,     s e   x ≠ 3 5 ,     s e   x = 3

Ver solução completa

Questão 146

12) Verifique se a função dada é contínua nos pontos indicados. Justifique a resposta.

f x =   x - 1 x - 1       ,         x ≠ 1   2                       ,       x = 1 em x = 1

Ver solução completa

Questão 147

15a) Para a função f definida por:

f x =   - 2 - x                                                   ,                                             x < 1 a x + b                                                           ,               1 ≤ x <   2           x 2 - 7 x + 12                             ,                                           x ≥ 2

Determine os valores de a e b para que f seja contínua em R

Ver solução completa

Questão 148

11c) Seja f definida por f x =   x 3 + 2 x 2 + x x 3 + 5 x 2 + 7 x + 3               s e     x ≠ - 3 ,   x ≠ - 1 0                                     s e   x =   - 3 - 1 2                             s e   x =   - 1

Dê os pontos onde f é descontínua. Justifique.

Ver solução completa

Questão 149

  1. Em cada item abaixo, esboce o gráfico de uma função f que satisfaz as condições do enunciado.

a) f é contínua em todos os pontos, exceto em x = 3 , onde o limite pela direita existe e é igual a f ( 3 ) .

Ver solução completa

Questão 150

11d) Seja f definida por f x =   x 3 + 2 x 2 + x x 3 + 5 x 2 + 7 x + 3               s e     x ≠ - 3 ,   x ≠ - 1 0                                     s e   x =   - 3 - 1 2                             s e   x =   - 1

A função f é contínua em R ? Justifique.

Ver solução completa

Questão 151

11b) Seja f definida por f x =   x 3 + 2 x 2 + x x 3 + 5 x 2 + 7 x + 3               s e     x ≠ - 3 ,   x ≠ - 1 0                                     s e   x =   - 3 - 1 2                             s e   x =   - 1

Dê os pontos onde f é contínua. Justifique.

Ver solução completa

Questão 152

3) Considere a função f : R → R definida por

f x = x - 1 6 x - 1 ,     s e   x ≠ 1 1 ,     s e   x = 1

Verifique que lim x → 1 - ⁡ f x = lim x → 1 + ⁡ f x . Então f é contínua em R ? Justifique.

Ver solução completa

Questão 153

23) Seja f   : R → R , tal que x s e n x ≤ f x ≤ x 2 cos 2 ⁡ x , ∀   x ∈ - π 2 , π 2 . Verifique se f é contínua em x = 0 .

Ver solução completa

Questão 154

29. Prove pela definição, que a função dada é contínua no ponto dado.

b) f x = x + 1 em p = 2

Ver solução completa

Questão 155

20) Verifique se a função é contínua no ponto indicado. Justifique a resposta.

f x =   x 3 ⋅ cos ⁡ 1 x             s e         x ≠ 0 1                                                 s e       x = 0

Em x =     0 .

Ver solução completa

Questão 156

Seja f a função definida por

f x = - 3 ,     s e   x < - 1 x 2 + 1 ,     s e - 1 ≤ x < 0 ( x + 1 ) ( x - 2 ) x - 2 ,     s e   0 ≤ x < 3 4 ,       s e   x ≥ 3

d) f é contínua no intervalo fechado - 1 2 , 1 ? Justifique.

Ver solução completa

Questão 157

Seja f a função definida por

f x = - 3 ,     s e   x < - 1 x 2 + 1 ,     s e - 1 ≤ x < 0 ( x + 1 ) ( x - 2 ) x - 2 ,     s e   0 ≤ x < 3 4 ,       s e   x ≥ 3

c) f é contínua em x = - 1 ? E em x = 2 ? Justifique.

Ver solução completa

Questão 158

Seja f: ⵏR ⟶ ⵏR definida por f ( x ) = { x 2 - 1 ,   s e   | x | ≤ 1 ;   1 - x 2 ,   s e   | x | > 1 .

(b) verifique se f ( x ) é contínua nos pontos -1 e 1?

Ver solução completa

Questão 159

2 – Dada a função f : R → R definida por

f x = 2 x + c ,     s e   x ≤ 1 x 2 + 3 x ,     s e   x > 1

Determine o valor de c para o qual f é contínua.

Ver solução completa

Questão 160

Determine onde cada uma das seguintes funções é descontínua:

f ( x ) = ( 1 - x ) / x 2   s e   x ≠ 0

1 , �� s e   x = 0

Ver solução completa

Questão 161

Determine onde cada uma das seguintes funções é descontínua:

f ( x ) = ( x 2 - x - 2 ) / ( x - 2 )   s e   x ≠ 2

1 ,   s e   x = 2

Ver solução completa

Questão 162

Determine os pontos que

f ( x ) = ( l n ( x ) + a r c t a n ( x ) ) / ( x 2 - 9 )

é contínua, e classifique suas descontinuidades.

Ver solução completa

Questão 163

  1. Determine os possíveis valores de a , b e c que tornam continuas as funções abaixo e esboce seus gráficos.

f x = 1 + x 2 ,   s e   x ≤ 0 b + x ,   s e   0 < x ≤ a x - a + c ,   s e   x > a

Ver solução completa

Questão 164

  1. Determine, caso possível, as constantes a ,   b ∈ R tais que f ( x ) seja contínua em x = 0 .

    2. f x = x + a 2 - 4 a - arctan ⁡ 11 x ,       x < 0 a - 1 ,                                         x = 0 sin ⁡ b x ln ⁡ 1 + 100 x ,       x > 0

  2. Encontre a equação da reta normal à curva y = 2 x - 3 e paralela à reta 9 x + 3 y - 5 = 0

Ver solução completa

Questão 165

  1. Seja f x = | x | se x for racional, e f x = 0 se x for irracional. Verifique se f é contínua em x = 0 .
  2. Considere a função f x = a 1 + a 2 cos ⁡ 2 x + a 3 cos ⁡ 4 x , onde a 1 ,   a 2 ,   a 3 são números reais. Sabendo que f 0 = f ' 0 = f ' ' 0 = f ' ' ' 0 e f π 2 = 1 , determine a 1 ,   a 2 ,   a 3 .

Ver solução completa

Questão 166

Considere a função

f x = x 2 - 1 ,     s e - 1 ≤ x < 0 2 x ,     s e   0 < x < 1 1 ,     s e   x = 1 - 2 x + 4 ,     s e   1 < x < 2 0 ,     s e   2 < x < 3

Responda:

  1. Existe f ( - 1 ) ?
  2. Existe lim x → - 1 + ⁡ f ( x ) ?
  3. lim x → - 1 + ⁡ f ( x ) = f ( - 1 ) ?
  4. f ( x ) é contínua em x = - 1 ?
  5. Existe f ( 1 ) ?
  6. Existe lim x → 1 ⁡ f ( x ) ?
  7. lim x → 1 ⁡ f ( x ) = f ( 1 ) ?
  8. f ( x ) é contínua em x = 1 ?

Ver solução completa

Questão 167

7. Dada a função f x = x 3 cos ⁡ 1 x ,     s e   x ≠ 0 0 ,     s e   x = 0

Mostre que:

b) f ' é continua.

Ver solução completa

Questão 168

Verifique a continuidade das funções abaixo nos pontos indicados. No caso de descontinuidade, classifique-a.

g x = x - x x ,     s e   x ≠ 0 0 ,                                           s e   x = 0             x = 0

Ver solução completa

Questão 169

Determine m ,   n ∈ R de modo que f x = - x 2 + n x - 3 x 3 - 27 ,           s e   x < 3 1 - m x + 1 x 3 ,           s e   x ≥ 3 seja contínua em x = 3 .

Ver solução completa

Questão 170

22) Verifique se existe a ∈ R tal que f x =   1 + a x             ,     x ≤ 0   x 4 + 2 a       ,       x > 0 seja contínua em R .

Ver solução completa

Questão 171

7 – Determine, se existirem, os valores de x para os quais cada uma das seguintes funções é descontínua:

b) g x = 1 x + 1 , s e   x > - 1 1 s e   x = - 1 x + 1 s e   x < - 1

Ver solução completa

Questão 172

7 – Determine, se existirem, os valores de x para os quais cada uma das seguintes funções é descontínua:

c) h x = x - 3 , s e   x ≠ 3 2 , s e   x = 3

Ver solução completa

Questão 173

Determine o valor de A para que a função f x seja contínua, com: f x = A x - 2 , x ≤ 0 - e x e x + 1 x > 0

Ver solução completa

Questão 174

  1. Em cada item abaixo, esboce o gráfico de uma função f que satisfaz as condições do enunciado.

b) f tem limite em x = 3 , mas não é contínua nesse ponto.

Ver solução completa

Questão 175

Determine a ,   b   ∈   R tal que a função f x = - 2 - x       s e   s e   x   <   1 , a x + b       s e   1   ≤   x   <   2 ,   x 2 - 7 x + 12     s e   x   ≥   2 ,   , seja contínua.

Ver solução completa

Questão 176

  1. Em cada item abaixo, esboce o gráfico de uma função f que satisfaz as condições do enunciado.

c) f não é contínua em x = 3 , mas torna-se contínua se seu valor em x = 3 for mudado para f 3 = 0 .

Ver solução completa

Questão 177

  1. Em cada item abaixo, esboce o gráfico de uma função f que satisfaz as condições do enunciado.

d) f é contínua no intervalo 0,3 , está definida em 0,3 mas não é contínua em 0,3 .

Ver solução completa

Questão 178

Sabe-se que lim x → 2 ⁡ f ( x ) = 5 e f está definida em R . Todas as afirmações abaixo são falsas. Desenhe um contra-exemplo para cada uma delas.

a) f ( x )   >   0 para x   ∈   ( 1 ,   3 )

b)   f 2 = 5

c) f ( 2 ) é positivo

Ver solução completa

Questão 179

  1. Dizemos que f tem uma descontinuidade removível no ponto x   =   a quando existe o limite lim x → a ⁡ f x mas f não é contínua ou não está definida neste ponto. Este é o caso da função f x = x 2     -   1 x   –   1     que não está definida em x   =   1 , mas satisfaz lim x → 1 ⁡ x 2 - 1 x - 1 = lim x → 1 ⁡ x + 1 = 2   Note que podemos incluir o ponto x = 1 no domínio fazendo f ( 1 )   =   2 . Com essa definição, a (nova) função f ´é contínua em x   =   1 . Para cada uma das funções abaixo, determine os (possíveis) pontos de descontinuidade removível.
    1. f x = x 2 + 3 x x + 3

Ver solução completa

Questão 180

Decida se as funções

f ( x ) x 3 cos ⁡ 1 x   s e   x ≠ 0 1   s e   x = 0

g ( x ) x - 1 x - 1   s e   x   ∈   [ 0 ,   1 )   ∪   ( 1 ,   + ∞ ) 1 / 2   s e   x = 1

são contínuas no ponto x = 0. Repita o exercício para x = 1.

Ver solução completa

Questão 181

  1. Lembrando que lim x → 0 ⁡ s e n x = 0 e lim x → 0 ⁡ c o s x = 1 , verifique que lim θ → 0 ⁡ s e n θ + a = s e n ( a ) . Conclua daí que a função seno é contínua

Ver solução completa

Questão 182

Considere

Verifique se f �� contínua em 1

Ver solução completa

Questão 183

Determine para quais valores de a função f definida abaixo é contínua em x = 1 .

f x = x 2 + a x ,   s e   x ≤ 1 a 2 x 2 - 1 ,   s e   x > 1

Ver solução completa

Questão 184

Use o mesmo raciocínio do exercício anterior para verificar que a função cosseno também é contínua. O que se pode dizer sobre a continuidade das demais funções trigonométricas?

Ver solução completa

Questão 185

A função maior inteiro é a função que associa, a cada elemento x   ∈   R , o valor [ [ x ] ] que é o maior número inteiro que é menor ou igual a x . Por exemplo,

[ [ 0 ,   5 ] ]   =   0 ,   [ [ 3 ] ]   =   3 ,   [ [ - 1 ,   8 ] ]   =   - 2 .

a) Calcule [ [ 3 ,   7 ] ] ,   [ [ - 0 ,   6 ] ] ,   [ [ n ] ] com n   ∈   N

(b) Estude os limites laterais da função maior inteiro no ponto x   =   2 . Em seguida, decida se ela é contínua neste ponto

(c) Determine todos os pontos onde a função não é contínua

(d) Faça um esboço do gráfico da função

Ver solução completa

Questão 186

Mostre que o polinômio p x =   x 6 - 7 x 3 + 2 x 2 + 3 possui pelo menos uma raíz real.

Ver solução completa

Questão 187

Q03a) Seja f : I R → I R dada por

f x = 4 x 2 + 3   ,     x ≥ 1 8 x - 2 ,     x < 1

A função f é contínua em x = 1 ? Justifique sua resposta

Ver solução completa

Questão 188

Determine o valor de c de forma que f seja contínua em R

f x = x 2 + 2 ,   s e   x ≤ 1 c x + 1 ,   s e > 1

Ver solução completa

Questão 189

7 – Determine, se existirem, os valores de x para os quais cada uma das seguintes funções é descontínua:

d) i x = 1 x - 5 , s e   x ≠ 5 0 , s e   x = 5

Ver solução completa

Questão 190

Seja f : R → R uma função contínua. Dois pontos de seu gráfico estão marcados no plano cartesiano abaixo. É possível garantir que existe x ∈ R tal que f x = 2 x ? Justifique.

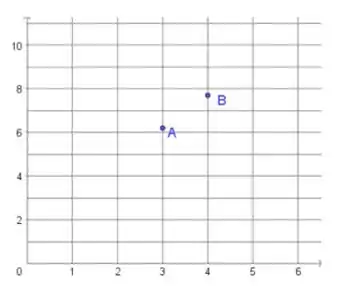
Atenção: As intersecções da malha são os pontos de coordenadas n , m ,   n ,   m naturais. O ponto A está ligeiramente acima do ponto ( 3,6 ) e o ponto B está ligeiramente abaixo do ponto ( 4,8 ) .

Ver solução completa

Questão 191

Determine valores para a , b ∈ R para que a função definida abaixo seja contínua em R . Justifique muito bem sua resposta:

f x =   b c o s x 2 x ,                       s e   x < 0 0 ,                                                     s e   x = 0 3 - s e n a x x ,           s e   x > 0

Ver solução completa

Questão 192

Seja f uma função definida em ℝ e suponha que exista uma constante M > 0 tal que

| f ( x ) - f ( p ) | ≤ M | x - p | 2 ,

para todo x ∈ ℝ .

( a ) Prove que f é contínua em p .

Ver solução completa

Questão 193

7.5 Explique por que a função é descontínua no ponto indicado, em seguida, esboce o gráfico da função, nos seguintes casos.

a) f x = e x ,     s e   x < 0 x 2 ,       s e   x ≥ 0 ponto a = 0 .

Ver solução completa

Questão 194

7.5 Explique por que a função é descontínua no ponto indicado, em seguida, esboce o gráfico da função, nos seguintes casos.

b) f x = x 2 - x x 2 - 1 ,     s e   x ≠ 1 1 ,       s e   x = 1 ponto a = 1 .

Ver solução completa

Questão 195

8.1 Determine o valor da constante a de modo que seja contínua a função dada por

f x = a 3 x 3 + 2 ,       s e   x < 1 a x + 8 ,       s e   x ≥ 1

Ver solução completa

Questão 196

Para cada uma das funções seguintes determine o(s) valor(es) de x para o(s) qual(quais) a função é descontínua. identifique o(s) tipo(s) de descontinuidade(s). Nos casos possíveis, encontra uma nova definição para a função de modo a remover qualquer (quaisquer) descontinuidade(s) removível (removíveis).

( c )   h ( x ) = e x + 4 x 3 e 4 x - 3

Ver solução completa

Questão 197

8.2 Determine onde cada uma das funções é descontínua:

a) f x = x 2 - x - 2 x - 2

Em seguida, classifique essas descontinuidades.

Ver solução completa

Questão 198

Para cada uma das funções seguintes determine o(s) valor(es) de x para o(s) qual(quais) a função é descontínua. identifique o(s) tipo(s) de descontinuidade(s). Nos casos possíveis, encontra uma nova definição para a função de modo a remover qualquer (quaisquer) descontinuidade(s) removível (removíveis).

( a )   f ( x ) = ( x - 1 ) 2 ( x - 1 ) ( x 2 - 4 x + 5 )

Ver solução completa

Questão 199

Para cada uma das funções seguintes determine o(s) valor(es) de x para o(s) qual(quais) a função é descontínua. identifique o(s) tipo(s) de descontinuidade(s). Nos casos possíveis, encontra uma nova definição para a função de modo a remover qualquer (quaisquer) descontinuidade(s) removível (removíveis).

( b )   f ( x ) = x - 2 ( x - 2 ) ( x 2 + 2 x + 10 )

Ver solução completa

Questão 200

Sabendo que lim u → 0 ⁡ sin ⁡ ( u ) u = 1 , obtenha o valor de a para que a função f ( x ,   y ) seja contínua

f x ,   y = sin ⁡ ( x 2 - y 2 ) x + y ,     s e   x ,   y ≠ ( 0 ,   0 ) a ,                                                               s e   x ,   y = ( 0 ,   0 )

Ver solução completa

Questão 201

Mostre que f ( x ) = x + 1 x é contínua para todo x > 0 .

Ver solução completa

Questão 202

Estude a continuidade da função

f ( x ) = x 2 - 7 x + 1 x 2 - 9

O que acontece quando x → ± 3 ?

Ver solução completa

Questão 203

30. Prove que f x = 1 x é contínua para todo p ≠ 0 .

Ver solução completa

Questão 204

31. A função

f x = 2 x   s e   x ≤ 1 1   s e   x > 1

É contínua em 1? Justifique.

Ver solução completa

Questão 205

Considere a função f : R → R   dada por

  1. Construa o gráfico de f ;

Ver solução completa

Questão 206

Determine, se existirem, valores de a ,   b para os quais a função abaixo seja contínua:

Ver solução completa

Questão 207

4. Seja

f x = f x = x 2 - x - 2 x - 2 ,     x ≠ 2 c ,     x = 2

b. A função f possui assíntotas verticais? Justifique!

Ver solução completa

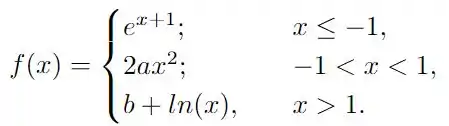
Questão 208

4. Seja

f x = f x = x 2 - x - 2 x - 2 ,     x ≠ 2 c ,     x = 2

  1. Determine um valor para constante c de forma que a função f seja contínua em R .

Ver solução completa

Questão 209

1. Use a continuidade para calcular o limite seguintes:

a) lim x → 3 ⁡ e x 2 - x

b) lim x → 2 ⁡ a r c t g x 2 - 4 3 x 2 - 6 x

Ver solução completa

Questão 210

  1. Dizemos que f tem uma descontinuidade removível no ponto x   =   a quando existe o limite lim x → a ⁡ f x mas f não contínua ou não está definida neste ponto. Este é o caso da função f x = x 2     -   1 x   –   1     que não está definida em x   =   1 , mas satisfaz lim x → 1 ⁡ x 2 - 1 x - 1 = lim x → 1 ⁡ x + 1 = 2   Note que podemos incluir o ponto x = 1 no domínio fazendo f ( 1 )   =   2 . Com essa definição, a (nova) função f   ´é contínua em x   =   1 . Para cada uma das funções abaixo, determine os (possíveis) pontos de descontinuidade removível.

b. f x = x | x |

Ver solução completa

Questão 211

  1. Dizemos que f tem uma descontinuidade removível no ponto x   =   a quando existe o limite lim x → a ⁡ f x mas f não contínua ou não está definida neste ponto. Este é o caso da função f x = x 2     -   1 x   –   1     que não está definida em x   =   1 , mas satisfaz lim x → 1 ⁡ x 2 - 1 x - 1 = lim x → 1 ⁡ x + 1 = 2   Note que podemos incluir o ponto x = 1 no domínio fazendo f ( 1 )   =   2 . Com essa definição, a (nova) função f   ´é contínua em x   =   1 . Para cada uma das funções abaixo, determine os (possíveis) pontos de descontinuidade removível.

c. f x = 5 ∙ s e n ( x ) x

Ver solução completa

Questão 212

Mostre que a função

é contínua na origem.

Ver solução completa

Questão 213

A função f ( x ) = | x | é contínua em todos os seus pontos (prove!).

Ver solução completa

Questão 214

  1. Dizemos que f tem uma descontinuidade removível no ponto x   =   a quando existe o limite lim x → a ⁡ f x mas f não contínua ou não está definida neste ponto. Este é o caso da função f x = x 2     -   1 x   –   1     que não está definida em x   =   1 , mas satisfaz lim x → 1 ⁡ x 2 - 1 x - 1 = lim x → 1 ⁡ x + 1 = 2   Note que podemos incluir o ponto x = 1 no domínio fazendo f ( 1 )   =   2 . Com essa definição, a (nova) função f ´é contínua em x   =   1 . Para cada uma das funções abaixo, determine os (possíveis) pontos de descontinuidade removível.

d. f x = x 2 - 1 x 3 - 1

Ver solução completa

Questão 215

Mostre que a função abaixo não é contínua na origem (tente procurar um δ e veja o que acontece)

Ver solução completa

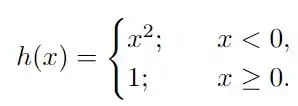
Questão 216

Seja f ( x ) uma função e suponha que para todo x ∈ R , f ( x ) ≤ x 2 . Calcule lim x → 0 ⁡ f ( x ) . A função é contínua na origem?

Ver solução completa

Questão 217

Seja a função

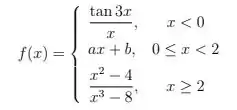
Determine os valores de a   e   b para que a função seja contínua

Ver solução completa

Questão 218

21) Verifique se a função é contínua no ponto indicado. Justifique a resposta.

f t =   1 - t 1 - ∛ t                 ,       s e   t ≠ 1 3 2                                         ,       s e   t = 1

Em t = 1 .

Ver solução completa

Questão 219

Sejam f , g : A ⊆ R → R com lim x → p ⁡ f x = 0 e g ( x ) ≤ M para todo x ∈ A , M fixado. Mostre que lim x → p ⁡ f x g ( x ) = 0 .

Ver solução completa

Questão 220

Seja

f x = x + 1 ,     x ≥ 1 2 x ,     x < 1

b) Existe lim x → 1 ⁡ f x - f ( 1 ) x - 1 ?

Ver solução completa

Questão 221

Seja

f x = x + 1 ,     x ≥ 1 2 x ,     x < 1

a) A função f ( x ) é contínua em x = 1 ?

Ver solução completa

Questão 222

Qual a semelhança entre o gráfico de

f x = x + 1 ,     x ≥ 1 2 x ,     x < 1

E o pato?

Ver solução completa

Questão 223

Seja f : R → R , tal que x 2 cos ² ⁡ x ≤ f x ≤ x sen ⁡ x , ∀ x ∈ - π 2 , π 2 . Verifique se f é contínua em x = 0 .

Ver solução completa

Questão 224

Determina a , b para que a função

f x =   a x + 2   ,                                         x > 1 x 2 - 4 x + 1   ,     x < 1 b   ,                                                           x = 1

seja contínua.

Ver solução completa

Questão 225

Seja f ( x ) uma função tal que para todo x ≠ 0 temos

cos ⁡ ( x ) - 1 ≤ f x ≤ x 4 + x 2

Calcule lim x → 0 ⁡ f ( x ) . Mostre que se f for contínua então f 0 = 0 .

Ver solução completa

Questão 226

Seja

h x = x + 2 + x - 2 x

a ) Determine o domínio de h ( x ) e escreva a expressão da função sem usar módulo. Verifique se a função é par ou ímpar, ou injetora. Justifique sua resposta provando ou dando contra-exemplo.

Ver solução completa

Questão 227

Dê condições suficientes e necessárias sobre α e β para que a função

f x =   α x - β   ,     x ≤ 1 , 3 x   ,     1 < x < 2 , β x 2 - α   ,     x ≥ 2

seja contínua.

Ver solução completa

Questão 228

Seja

f x = x 5 + 4 x 5 + x 3 + x + 2 ,   x ≥ 0 β cos ⁡ x ,   x < 0

  1. Existe algum valor de β que torna f é contínua em x = 0 ? Justifique sua resposta

Ver solução completa

Questão 229

Considere as funções abaixo e determine se são contínuas para o valor de x dado.

f x = x + 2 x + 1                       p a r a   x = 1

Ver solução completa

Questão 230

Considere as funções abaixo e determine se são contínuas para o valor de x dado.

f x = s e n ( π )                   p a r a   x = 2

Ver solução completa

Questão 231

A função f é contínua em x   =   2 ? Justifique sua resposta.

f ( x ) = 5 x + 2 2 x - 1   s e   x ≥ 2

= 10 x - 3   s e   x < 2

Ver solução completa

Questão 232

Encontre o domínio das seguintes funções:

d) p x = 1 x 2 - 4 + 3 x 2 + 1 3 - x

Ver solução completa

Questão 233

Seja f a função definida por:

f x = x + 2 ,     s e   x < - 2 x 2 + x - 2 ,     s e - 2 ≤ x ≤ 1 4           ,     s e   x > 1

Determine o domínio de f , esboce seu gráfico e determine sua imagem, I m ( f ) .

Ver solução completa

Questão 234

Encontre o domínio das seguintes funções:

a) f x = - 4 x 3 - 1 2 x 2 - 3 x + 2022

Ver solução completa

Questão 235

Encontre o domínio das seguintes funções:

b) g x = 3 x 2 - 5 x + 7 x 2 - 9

Ver solução completa

Questão 236

Para que a função f : R → R seja contínua em R , o valor de m n deve ser:

f x = 3 x 2 - 7 x + 2 ,   s e   x > 1 m x + n ,   s e - 1 ≤ x ≤ 1 s e n π x 2 ,   s e   x < - 1

Ver solução completa

Questão 237

  1. Estude, em função dos valores α ∈ R , a continuidade da função f : R 2 → R ,   dada por

    2. f x , y = x 4 + 2 x 2 y 2 + α y 4 cos ⁡ x 2 + α y 2 - 1 ,         x , y ≠ ( 0,0 ) - 2 α ,         x , y = ( 0,0 )

  2. Analise a diferenciabilidade de f ( x , y ) em ( 0,0 ) para os casos de α = 0 e α = 1 .

Ver solução completa

Questão 238

Para cada gráfico da figura 1.3 , determine se a função traçada é contínua no intervalo - 1,3 . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

Ver solução completa

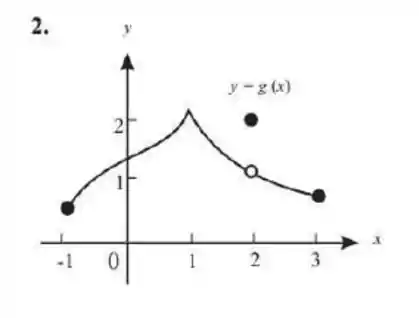
Questão 239

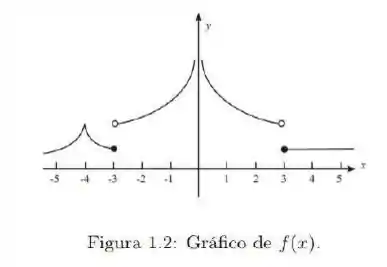
Observando o gráfico de f ( x ) na figura abaixo, determine se a função é contínua ou descontínua em cada um dos seguintes valores de x

  1. x = - 1
  2. x = - 4
  3. x = - 3
  4. x = 3
  5. x = 4

Ver solução completa

Questão 240

1.3 , determine se a função traçada é contínua no intervalo - 1,3 . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

Ver solução completa

Questão 241

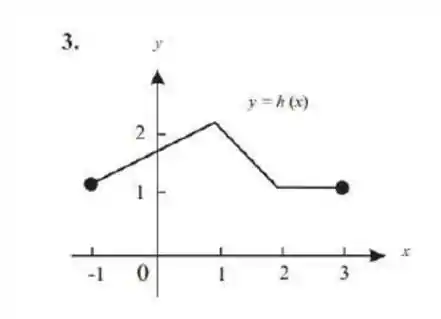
Para cada gráfico da figura 1.3 , determine se a função traçada é contínua no intervalo - 1,3 . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

Ver solução completa

Questão 242

Determine se as seguintes funções são contínuas em D ( f ) :

c )   h x = x 2 - 9 x - 3 ,     s e   x ≠ 3 6 ,     s e   x = 3  

Ver solução completa

Questão 243

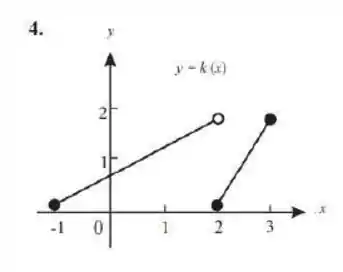
Para cada gráfico da figura 1.3 , determine se a função traçada é contínua no intervalo - 1,3 . Se não for contínua, aponte onde ela deixa de ser contínua e diga qual o tipo de descontinuidade em questão.

Ver solução completa

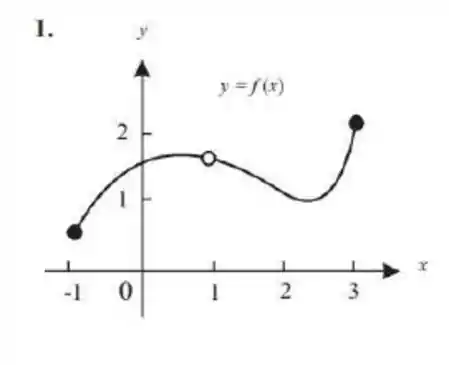
Questão 244

Determine os possíveis valores de a e b que tornam contínuas as funções abaixo.

f x = a x 2 + 2 x           s e   x < 2 x 3 - a x                 s e   x ≤ 2

Ver solução completa

Questão 245

Determine, se existirem, os valores de x para os quais cada uma das seguintes funções é descontínua

a )   f x = 3 - x ,         s e   x < 1 4 ,                     s e   x = 1 x 2 + 1 ,     s e   x > 1

Ver solução completa

Questão 246

Determine L para que a função f definida abaixo seja contínua em x = 5 .

f x = x - 5 x + 5 - 10 ,   s e   x ≠ 5 L ,   s e   x = 5

Ver solução completa

Questão 247

Determine os possíveis valores de a e b que tornam contínuas as funções abaixo.

f x = x 2 - 4 x - 2           s e   x < 2 , a x 2 - b x + 3         s e   2 ≤ x < 3 , 2 x - a + b           s e   x ≥ 3 .

Ver solução completa

Questão 248

A função

f ( x ) = x 2 s i n ( 1 / x )   s e   x ≠ 0

e

= 0   s e   x = 0

é da classe C 2

Ver solução completa

Questão 249

Para cada afirmação, assinale V se ela for verdadeira, ou F se ela for falsa

( ) Toda função polinomial é contínua em R

( ) Se f x for contínua em a , então lim x → a ⁡ f x = f a

( ) Para uma função f ( x ) , se D f = R , então f é contínua em toda parte

( ) Toda função racional possui descontinuidade onde o denominador é zero

Ver solução completa

Questão 250

4.6. A função

k x = x 2 + 1 ,     x ∈ Q x + 1 ,     x ∈ R / Q

é contínua em apenas dois pontos.

Ver solução completa

Questão 251

4.7. Em quais pontos a função

k x = cos ⁡ x ,     x ∈ Q s e n x ,     x ∈ R / Q

é contínua?

Ver solução completa

Questão 252

Determine os pontos de continuidade de cada uma das funções abaixo

a ) f x = sin ⁡ x 2 - 4 + 5 ,   s e   x > 2 x 2 + x - 6 x - 2 ,   s e   x < 2 5 ,   s e   x = 2

Ver solução completa

Questão 253

Encontre o domínio das seguintes funções:

c) h x = x 2 - 4 x + 3

Ver solução completa

Questão 254

Verifique a continuidade das funções abaixo no ponto 0,0 .

b) g x , y =   x 2 - y 2 x 2 + y 2 ,           s e   x , y ≠ ( 0,0 ) 0 ,                         s e   x , y = ( 0,0 )

Ver solução completa

Questão 255

Determine os possíveis valores de a, b e c que tornam contínuas as funções abaixo.

f x = 1 + x 2         s e   x ≤ 0 b + x       s e   0 < x ≤ a x - a + c         s e   x > a

Ver solução completa

Questão 256

Encontre os pontos onde há descontinuidade no gráfico

Ver solução completa

Questão 257

Diga em qual região as funções abaixo são contínuas. Se ela for descontínua em um ponto ou região, diga o motivo da descontinuidade.

a) f x ,   y ,   z = 1 x 2 + y 2 + z 2

Ver solução completa

Questão 258

Diga em qual região as funções abaixo são contínuas. Se ela for descontínua em um ponto ou região, diga o motivo da descontinuidade.

b) f x ,   y ,   z = z x 2 + y 2 - 4

Ver solução completa

Questão 259

Diga em qual região as funções abaixo são contínuas. Se ela for descontínua em um ponto ou região, diga o motivo da descontinuidade.

c) f x ,   y ,   z = sin ⁡ z e x + e y

Ver solução completa

Questão 260

Diga em qual região as funções abaixo são contínuas. Se ela for descontínua em um ponto ou região, diga o motivo da descontinuidade.

d) f x ,   y ,   z = x y sin ⁡ ( z )

Ver solução completa

Questão 261

Diga em qual região as funções abaixo são contínuas. Se ela for descontínua em um ponto ou região, diga o motivo da descontinuidade.

e) f x ,   y = sin ⁡ x y x y ,     x y ≠ 0 1 ,                         x y = 0

Ver solução completa

Questão 262

Considere as funções abaixo e determine se são contínuas para o valor de x dado.

f x = k                       p a r a   x = 5

Ver solução completa

Questão 263

Considere as funções abaixo e determine se são contínuas para o valor de x dado.

f x = x 2 + x ,       s e   x < 1 3 ,                         s e   x = 1 x 2 - 1 x + 1 ,       s e   x > 1 ;                   p a r a   x = 1

Ver solução completa

Questão 264

2. Seja f uma função contínua (isto é, contínua em todos os pontos do seu domínio). Sabe-se que f 0 = 3 , f 2 = 0 e f 3 = - 2 . Calcule os limites de lim x → 0 ⁡ f ( x ) , lim x → 2 - ⁡ f ( x ) e lim x → 3 + ⁡ f ( x )

Ver solução completa

Questão 265

3. Em cada item, use as propriedades de continuidade para explicar por que a função é contínua em seu domínio.

  1. f x = x 2 - 3 x + 4 e x
  2. f x = 2 sin ⁡ x - x 2 - 9 x - 3

Ver solução completa

Questão 266

5. Sejam a e b números reais tais que a função

f x = x 3 - a x 2 + b x x + 5 15 ,     x = - 5 ,     x ≠ - 5

É contínua. Calcule f 6 .

Ver solução completa

Questão 267

2. Calcule o valor de α ∈ R para que a função f seja contínua em x = 0 , onde

f x = tan ⁡ x - sin ⁡ x x 5 + 4 x 3 ,   s e   x ≠ 0 α   ,   s e   x = 0

Ver solução completa

Questão 268

  1. Determine os possíveis valores de a , b e c que tornam continuas as funções abaixo e esboce seus gráficos.

f x = sin ⁡ ( b x + b ) a x + a ,   s e   x < - 1 3 x + 1 ,   s e - 1 ≤ x ≤ 0 a ln ⁡ x + e x + 1 ,   s e   x ≥ 0

Ver solução completa

Questão 269

Determine os valores das constantes a e b para que a função f , dada abaixo, seja contínua em [ - 3 ,   3 ] .

f x = a ,     x = - 3 9 - x 2 4 - x 2 + 7 ,   - 3 < x < 3 b ,     x = 3

Ver solução completa

Questão 270

Dada a função f x = 2 - x 2 + 7 3 x 3 - 1 para x ≠ 1 , defina o valor de g ( 1 ) para que a função g seja contínua em x = 1 , se g x = f ( x ) para x ≠ 1 .

Ver solução completa

Questão 271

Determine os valores de a e b para que a função f , dada abaixo, seja contínua em R .

f x = x 4 ,     x ≤ - 1 a x + b ,   - 1 < x < 2 x 2 + 3 ,     x ≥ 2

Ver solução completa

Questão 272

Determine a   ∈   R tal que a função

f ( x ) 1 + a x             s e   x ≤ 0 , x 4 + 2 a         s e   x > 0 ,

Seja contínua em x   =   0 .

Ver solução completa

Questão 273

Seja f a função definida por:

f x =   x 2 - a x + 3 x - 1 ,       s e   x < 1 b x + 1 ,       s e   x ≥ 1

Determine os valores de a e b para que f seja contínua.

Ver solução completa

Questão 274

Determine um valor para a constante k , se possível, que torna a função

f x = k x 2 ,       s e   x ≤ 2 2 x + k ,       s e   x > 2

contínua

Ver solução completa

Questão 275

Encontre L tal que a função abaixo seja contínua em x = - 1

f x = L + e x + 1 cos ⁡ x + 1   ,     s e   x ≥ - 1 3 x 3 + 3 x + 2   ,     s e   x < - 1

Ver solução completa

Questão 276

Seja f   : R   →   R , tal que:

x 2 c o s 2 ( x )   ≤   f ( x )   ≤   x   s e n ( x )

Para todo x ∈ ( - π / 2 , π / 2 ).

Mostre que f é contínua em x   =   0  

Ver solução completa

Questão 277

Determine o valor da constante c para que a função f , dada abaixo, seja contínua em [ 0 ,   + ∞ ) .

f x = x 2 + 16 - 5 4 - x 2 + 7 ,     x > 0   e   x ≠ 3 c ,     x = 3

Ver solução completa

Questão 278

Determine o valor da constante c para que a função f , dada abaixo, seja contínua em x = 0 .

f x = 1 - cos ⁡ x sin 2 ⁡ x ,         x ≠ 0 c ,     x = 0

Ver solução completa

Questão 279

Encontre os valores de a , b e c para que os gráficos das funções definidas por f ( x )   =   x ²   +   a x +   b e g ( x )   =     x 3 -   2 x 2 3   +   c se interceptem no ponto ( 1,2 ) e tenham a mesma reta tangente neste ponto.

Ver solução completa

Questão 280

Determine, se existir, o valor L ∈ R para que cada uma das funções abaixo seja contínua

a ) f x = sin ⁡ x 2 + 2 - sin ⁡ ( x + 2 ) x ,   s e   x ≠ 0 L ,   s e   x = 0

Ver solução completa

Questão 281

Determine, se existir, o valor L ∈ R para que cada uma das funções abaixo sejam contínuas

b ) f x = x 8 + x 4 x 2 ,   s e   x ≠ 0 L ,   s e   x = 0

Ver solução completa

Questão 282

Sejam f , g : R → R tais que:

(i) f é contínua em x = 0 e

(ii) g é descontínua em x = 0.

Pode-se concluir corretamente que é descontínua em x = 0 a função:

a. f + g; b. f g; c. f ◦ g; d. g ◦ f ; e. |g|.

Ver solução completa

Questão 283

Determine os pontos de continuidade de cada uma das funções abaixo

b ) f x = x 2 - 4 x + 3 x - 3 ,   s e   x ≠ 3 1 ,   s e   x = 3

Ver solução completa

Questão 284

Determine os pontos de continuidade de cada uma das funções abaixo

c ) f x = 1 + - 1 x 2 sin ⁡ π x ,   o n d e   x   é   o   m a i o r   i n t e i r o   m e n o r   o u   i g u a l   a   x

Ver solução completa

Questão 285

Seja f : R → R a função dada por f(x) = { x 2 , se x ∈ Q; x 3 , se x ∈ R \ Q.

O conjunto descontinuidades de f é: a. ∅; b. Q; c. R \ Q; d. R \ {0}; e. R.

Ver solução completa

Questão 286

Para que a função f ( x )   = {         | x   2   +   2 x   −   3 | x - 1   , se x   <   1 ; x �� +   k , se x   ≥   1 . seja contínua em R o valor da constante k deve ser:

a. −7; b. 1; c. 3; d. −1; e. −5.

Ver solução completa

Questão 287

Construa uma função f : R → R que é contínua em um único ponto.

Ver solução completa

Questão 288

Construa uma função f : R → R que é contínua somente em dois pontos.

Ver solução completa

Questão 289

Seja f uma função real tal que |   f ( x ) |   ≤   |   s i n ( x ) | para todo x   ∈   R . Então

a. f pode ser descontínua em x = 0 ;

b. f é contínua em x = 0 , mas pode não ser derivável em x = 0 ;

c. f é derivável em x = 0 e   f   ′   ( 0 )   = 0 ;

d. f é derivável em x = 0 e   f   ′   ( 0 )   = 1 ;

e. f é derivável em x = 0 mas podemos apenas afirmar que − 1   ≤   f   ′   ( 0 )   ≤ 1 .

Ver solução completa

Questão 290

Sabendo que f   :   R   →   R é derivável em a   ∈ ] 0 ,   + ∞ [ , calcule l i m x → a f ( x ) - f ( a ) x - a em termos de f   ′ ( a ) .

Ver solução completa

Questão 291

Existe um valor α tal que a função f ( x )

g ( x ) = 1 - 1 + A x B x 1 + A x

seja contínua em x = 0 ?

Ver solução completa

Questão 292

Considere a função f(x) = x|x|. Decida se f é derivável em x 0 = 0 e calcule f′(0) em caso afirmativo.

Ver solução completa

Questão 293

Dê um exemplo com duas funções f e g tais que f seja contínua em x = 0 , g seja descontínua em x = 0 e no entanto f . g seja contínua em x = 0 .

Ver solução completa

Questão 294

Definia se f é contínua em a

Ver solução completa

Questão 295

Responda as seguintes perguntas (justifique suas respostas):

  1. Será que a equação x 3 + e x - 1 4 = 0 tem solução real?

Ver solução completa

Questão 296

Dada f ( x , y ) =   0 ,   s e   ( x , y )   =   ( 0,0 ) ; e f ( x , y ) = 2 x y 2 x ² + 2 y ²

  1. Determine se f é contínua na origem.

Ver solução completa

Questão 297

41. Seja f x = x 5 + x + 1 . Justifique a afirmação: f tem pelo menos uma raiz no intervalo - 1,0 .

Ver solução completa

Questão 298

Determine o valor da constante c para que a função f , dada abaixo, seja contínua em [ 0 ,   + ∞ ) .

f x = x + x - 2 x - 1 ,     0 < x < 1 c x + 5 x 2 + 3 ,     x ≥ 1 .

Ver solução completa

Questão 299

Determine os pontos de descontinuidade da função a seguir

Ver solução completa

Questão 300

2) Seja

h t = t - 2 d 3 , s e   t < 0 ; c - d cos ⁡ t , s e   0 ≤ t ≤ π / 2   ; d sen ⁡ t + 2 , s e   t > π / 2 .

Determine os valores de c e d para os quais h é contínua.

Ver solução completa

Questão 301

Determine o valor da constante c para que a função f , dada abaixo, seja contínua em [ 2 ,   + ∞ ) .

f x = x 2 - 4 x 2 - 3 x + 2 ,     x > 2 c ,     x = 2

Ver solução completa

Questão 302

De o domínio da função

f ( x   ) = l n ( x + 4 ) + x 3

Ver solução completa

Questão 303

De o domínio da função

x ² + x - 6 x ² - 2 x

Ver solução completa

Questão 304

De o domínio da função

f ( x   ) = x ² + 3 x + 2

Ver solução completa

Questão 305

Decida se a afirmação é verdadeira ou falsa, justificando ou apresentando um contra-exemplo.

a. Se f : R → R é tal que | f | é contínua em x = 0, então f é contínua em x = 0.

b. Se f e g são funções descontínuas em x = 0, então a função f g é descontínua em x = 0.

Ver solução completa

Questão 306

Seja f ( x )   =     x 3 s i n ( 1 | x | ) | x | , se x ≠   0 ; 0, se x   =   0 .

Em x 0   =   0 pode-se afirmar que f é

a. descontínua;

b. derivável e f   ′   ( 0 )   =   1 ;

c. contínua mas não derivável;

d. derivável e f   ′   ( 0 )   =   0 ;

e. derivável e f   ′   ( 0 )   = - 1 .

Ver solução completa

Questão 307

Suponha que f : 0,1 → R é contínua e que 0 ≤ f x ≤ 1 , para todo x ∈ 0,1 . Prove que existe c ∈ 0,1 tal que f c = c .

Ver solução completa

Questão 308

Considere as seguintes afirmações:

I . Se g é limitada e lim x → + ∞ ⁡ f ( x ) = + ∞ , então lim x → + ∞ ⁡ g x f ( x ) = + ∞ .

I I . Se f : R → R é uma função tal que f x - f ( y ) ≤ x - y 2 então, f é derivável.

I I I . Se g : R → R é descontínua em x 0 e limitada então, f x = x g x sin ⁡ ( x ) é derivável em x 0 = 0 .

São corretas

a. nenhuma das afirmações;

b. todas as afirmações;

c. somente as afirmações I e I I ;

d. somente as afirmações I e I I I ;

e. somente as afirmações I I e I I I .

Ver solução completa

Questão 309

Suponha que f : 0,1 → R é contínua, f 0 = 1 e f x é um número racional para todo o x ∈ 0,1 . Prove que f x = 1 , para todo x ∈ 0,1 .

Ver solução completa

Questão 310

Determine L para que a função seja contínua no ponto dado. Justifique.

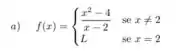
em p = 2

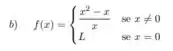
em p = 0

Ver solução completa

Questão 311

Para a função f cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique porquê.

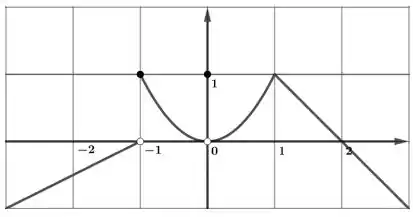
e) A função é contínua em x = 0 ?

Ver solução completa

Questão 312

Seja f : R → R , tal que:

f x = x 2 - 2 ,     x ≤ 4 8 x ,     x > 4

Calcule, caso exista, lim x → 4 ⁡ f x - f 4 x - 4 . Essa função é contínua em x = 4 ?

Ver solução completa

Questão 313

Considere a função f : R → R dada por f x = e - 1 / x 2   ,     s e   x ≠ 0 0                             s e   x = 0

a) Mostre que f é contínua em x = 0 .

b) Decida se f é derivável em x = 0 . Em caso afirmativo, calcule f ' ( 0 ) .

c) Esboce, no sistema de coordenadas abaixo, o gráfico de f , determinando os intervalos de crescimento, concavidade e limites necessários.

Ver solução completa

Questão 314

Seja g uma função contínua no intervalo [ - 1 ,   2 ] e derivável em ] - 1 ,   2 [ , que assume os valores

g - 1 = 0                 g 0 = 4                 g 1 = 2               g 2 = 2

Considere as afirmações:

I A equação g x = 3 tem pelo menos uma solução no intervalo [ - 1 ,   0 ] .

I I A equação g x = 2 tem exatamente uma solução no intervalo [ - 1 ,   0 ] .

I I I A função g admite um ponto crítico no intervalo ] 1 ,   2 [ .

Pode-se dizer com certeza que:

a. todas as afirmações são falsa.

b. somente as afirmações I e I I I são verdadeiras.

c. somente as afirmações I e I I são verdadeiras.

d. todas as afirmações são verdadeiras.

e. somente a afirmação I é verdadeira.

Ver solução completa

Questão 315

Seja f x , y = x x 2 + y 2 - 3 / 2 e sin ⁡ ( x 2 y ) . Calcule ∂ f ∂ x ( 1,0 )

Ver solução completa

Questão 316

Determine os pontos de continuidade da função

Ver solução completa

Questão 317

2. Seja f : R → R uma função que, em todo - 1 ≤ x ≤ 1 , vale s e n ⁡ ( x ) 1 + x 2 ≤ f ( x ) ≤ 2 x - x 2 4 - x 2 .

Verifique se pode garantir que  f  é contínua em  x = 0 .

Ver solução completa

Questão 318

Considere a função

f x = x + x 3 sin ⁡ 1 x ,     x ≠ 0 0 ,     x = 0

b) f é uma função contínua em todo o seu domínio?

Ver solução completa

Questão 319

Responda as seguintes perguntas (justifique suas respostas):

  1. Será que toda função que é contínua também é diferenciável?

Ver solução completa

Questão 320

Determine os possíveis valores de a, b e c que tornam contínuas as funções abaixo.

f x = sin ⁡ b x + b a x + a         s e   x < - 1 , 3 x + 1       s e - 1 ≤ x ≤ 0 , a ln ⁡ x + e x + 1 + b         s e   x > 0

Ver solução completa

Conteúdos Complementares

Conceitos de Continuidade

Função contínua

Listas de Exercícios Resolvidos

Lista de Polinômio de Taylor para f(x,y)Lista de Caso AvançadoLista de Erro do Polinômio de Taylor para f(x)Lista de Wronskiano - Dependência e Independência LinearLista de Caso Vetorial no R³Lista de Limites Laterais e Existência do LimiteLista de Caso Escalar R²Lista de Área de Superfícies de RevoluçãoLista de Área entre Curvas Lista de Curvas de Nível

Principais Conceitos de Cálculo

PrimitivasEquação da ElipseFunção contínuaCoeficiente LinearDiagrama De VennFórmula do x e y do vérticeTabelas de Relações TrigonométricasTabela de DerivadasPropriedades do Logaritmo - Tabela