Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.5 - Ex. 25

Nos Exercícios 25-28, esboce a curva juntamente com e a reta tangente no ponto dado. Em seguida, escreva uma equaçãopara a reta tangente.

Passo 1

Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Para esboçar a curva, precisamos primeiro achar o gradiente da função, aplicada ao ponto dado. Ou seja, temos que achar o vetor gradiente. Ele é dado por:

Dessa forma, para a nossa função, temos:

Shoooow. Agora é aplicar ao ponto . Para isso, substituiremos na nossa função gradiente. Ou seja:

Passo 2

Dessa forma, a linha tangente é dado por:

Não sabe como fazer isso? Relaxa que eu te ensino. Temos que substituir pelos valores que achamos do gradiente aplicado ao ponto, dado por:

Substituindo:

Simplificando:

Esboçando o que fizemos:

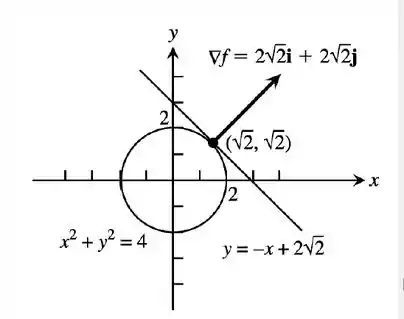
E é isso my good green fellas, até a próximas xuxuzinhos

Resposta

Esboço no passo 2

Exercícios de Livros Relacionados

3. Seja σ: Ω ⊂ ℝ2 → ℝ3, Ω aberto, uma superfície de classe C1 dada por σ(u, v) = (x (u, v), y (u, v), z (u, v)). Verifique que d σ d u × d σ d v = d y , z d u , v ,d z , x d u , v ,d x , y d u , v

Seja σ : Ω → R 3 , Ω aberto em R 2 , uma superfície de classe C 1 e seja γ : I → Ω uma curva de classe C 1 , com γ t = u t , v t . (Observe que γ t é um ponto de Ω , para todo t ∈ I .) Seja Γ : I → I

Nos Exercícios 25-28, esboce a curva f ( x ,y )=c juntamente com ∇ f e a reta tangente no ponto dado. Em seguida, escreva uma equaçãopara a reta tangente. x 2 - x y + y 2 = 7 - 1 , 2

Nos Exercícios 25-28, esboce a curva f ( x ,y )=c juntamente com ∇ f e a reta tangente no ponto dado. Em seguida, escreva uma equaçãopara a reta tangente. x 2 - y = 1 , 2 , 1

Nos Exercícios 25-28, esboce a curva f ( x ,y )=c juntamente com ∇ f e a reta tangente no ponto dado. Em seguida, escreva uma equaçãopara a reta tangente. x y = - 4 2 , - 2