Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.6 - Ex. 17

Nos Exercícios 13-18, encontre equações paramétricas para a reta tangente à curva de interseção das superfícies no ponto determinado

S u p e r f i c i s : x 3 + 3 x 2 y 2 + y 3 + 4 x y - z 2 = 0

x 2 + y 2 + z 2 = 1 1

Ponto:

( 1,1 , 3   )

Passo 1

Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Para as equações paramétricas, vamos precisar do gradiente da nossa função. Ele é dado por:

∇ f = δ f δ x i + δ f δ y j + δ f δ z j

Dessa forma, para a nossa função, temos:

∇ f = 3 x 2 + 6 x y 2 + 4 y i + 6 x 2 + 3 y 2 + 4 x j - 2 z k

Aplicado ao ponto:

∇ f 1 , 1,3 = 13 i + 13 j - 6 k

Passo 2

A partir disso, podemos tomar a linha tangente, parametrizada através de:

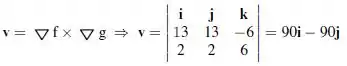
Logo,

l i n h a   t a n g e n t e : x = 1 + 90 t ,   y = 1 - 90 t ,   z = 3

Resposta

l i n h a   t a n g e n t e : x = 1 + 90 t ,   y = 1 - 90 t ,   z = 3

Exercícios de Livros Relacionados

Suponha que z = f ( x , y ) é uma função de classe C 1 , f 1,3 = - 1 , ∂ f ∂ x 1,3 = 4 e ∂ f ∂ y 1,3 = - 3 . Sabe-se que a curva σ t = t 2 , 4 t - 1 , z t , t ∈ R , está contida no gráfico da função z
Nos Exercícios 13-18, encontre equações paramétricas para a reta tangente à curva de interseção das superfícies no ponto determinado S u p e r f i c i s : x y z = 1 ,x 2 + 2 y 2 + 3 z 2 = 6 Ponto: ( 1
Nos Exercícios 13-18, encontre equações paramétricas para a reta tangente à curva de interseção das superfícies no ponto determinado S u p e r f i c i s : x + y 2 + 2 z = 4 x = 1 Ponto: ( 1,1 , 1 )
Nos Exercícios 13-18, encontre equações paramétricas para a reta tangente à curva de interseção das superfícies no ponto determinado S u p e r f i c i e s : x 2 + y 2 = 4 x 2 + y 2 - z = 0 Ponto: ( 2
Nos Exercícios 13-18, encontre equações paramétricas para a reta tangente à curva de interseção das superfícies no ponto determinado S u p e r f i c i s : x 2 + 2 y + 2 z = 4 y = 1 Ponto: ( 1,1 , 1 /