Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.5 - Ex. 6
6 -
Passo 1
O erro no método de Euler e no método de Runge-Kutta é diferente. Basicamente, o erro no método Euler é superior ao método Runge-Kutta de ordem superior. Como no método de ordem superior, o erro de truncamento é menor.
Passo 2
O problema do valor inicial em uma notação vetorial pode ser escrito como,
- A fórmula de Euler é,
-
Foi fornecido que temos:
O método Runge-Kutta inclui os seguintes cálculos:
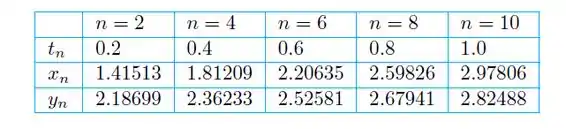
Com , os valores obtidos são os seguintes:
Passo 4
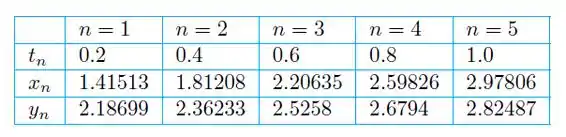
Isso é,
Com obter valores são os seguintes:
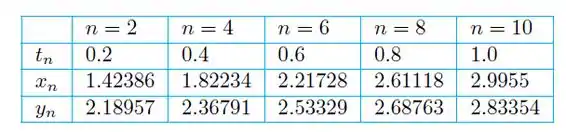
Passo 3
Com , os valores obtidos são os seguintes:
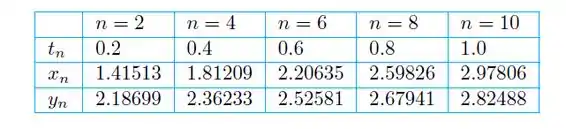
Resposta
a)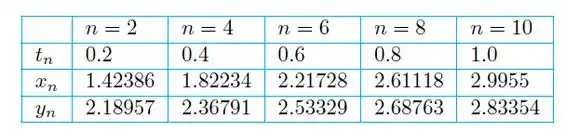 
b)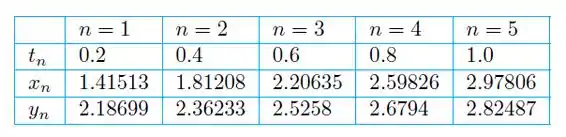 
c) 
Exercícios de Livros Relacionados
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular7. x 2 y ″ + 6 x y ' - y=0
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular3. x 2 y ″-3 x y '+4 y=0
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular4. x 2 y ″ +3 x y '+5 y=0
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular8. 2 x 2 y ″ - 4 x y ' + 6 y=0
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular2. ( x + 1 ) 2 y ″ + 3 ( x + 1 ) y ' + 0,75 y=0