Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.6 - Ex. 3

3 - Considere novamente o problema de valor inicial (16) do Exemplo 2. Investigue o quão pequeno tem que ser o tamanho do passo h para garantir que o erro em t   =   0,05 e em t = 0,1

seja menor do que 0,0005 .

(a) Use o método de Euler.

(b) Use o método de Euler inverso.

(c) Use o método de Runge-Kutta.

Passo 1

  1. Considere o problema do valor inicial

y ' = - 100 y + 100 t + 1 ,       y 0 = 1

E sua solução exata é,

y = ϕ t = e - 100 t + t

Cada etapa do método Euler é dada por:

y n + 1 = y n + h f ( t n , y n )

Resolva o problema com uma variedade de valores  h  revela que o erro é maior que 0,0005 .

Por  h = 0,0005 e menos que 0,0005 para h = 0,00025 .

Passo 2

b)

Cada etapa do método de Euler para trás é dada por

y n + 1 = y n + h f ( t n + 1 , y n + 1 )

Substitua na expressão por  f  e resolva para  y n + 1 :

y n + 1 = y n + h - 100 y n + 1 + 100 t n + 1 + 1

y n + 1 = y n + h 100 t n + 1 + 1 / ( 1 + 100 h )

Resolver o problema com uma variedade de valores  h  revela que o erro é maior que 0,0005 para  h = 0,0005 e menor que 0,0005 para h = 0,00025 .

A comparacção é mostrada abaixo:

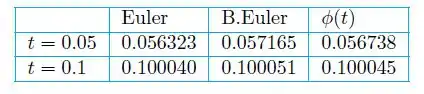
Passo 3

  1. Cada etapa do método Runge-Kutta é dada por:

y n + 1 = y n + h 6 k 1 + 2 k 2 + 2 k 3 + k 4

Onde:

k 1 = f ( t n , y n )

k 2 = f t n + h 2 , y n + h k 1 2

k 3 = f t n + h 2 , y n + h k 2 2

k 4 = f t n + 1 , y n + h k 3

Para h = 0,1 temos:

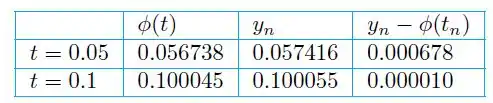
Para h = 0,005 temos:

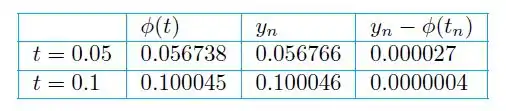
Resolver o problema com uma variedade de valores  h  revela que o erro é maior que 0,0005 para  h = 0,001 e menor que 0,0005 para h = 0,005 .

Resposta

  1. o problema com uma variedade de valores  h  revela que o erro é maior que 0,0005 .

    2. Por  h = 0,0005 e menos que 0,0005 para h = 0,00025 .

  2. o problema com uma variedade de valores  h  revela que o erro é maior que 0,0005 para  h = 0,0005 e menor que 0,0005 para h = 0,00025 .

  3. o problema com uma variedade de valores  h  revela que o erro é maior que 0,0005 para  h = 0,001 e menor que 0,0005 para h = 0,005 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular11. x 2 y ″ + 2 x y ' + 4 y=0
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular9. x 2 y ″ - 5 x y ' + 9 y=0
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular10. ( x - 2 ) 2 y ″ + 5 ( x - 2 ) y ' + 8 y=0
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular12. x 2 y ″ - 4 x y ' + 4 y=0
Em cada um dos problemas de 1 a 12, determine a solução geral da equação diferencial dada, válida em qualquer intervalo que não inclui o ponto singular5. x 2 y ″ - x y '+y=0