Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 8
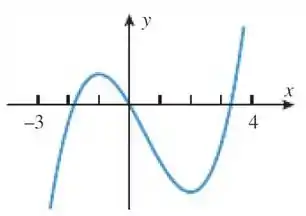
- Explique por que a função , cujo gráfico está na figura abaixo, não tem inversa em seu domínio .
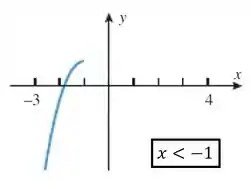
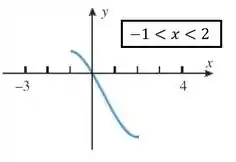
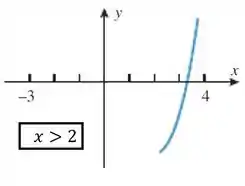
- Subdivida o domínio em três intervalos adjacentes sobre cada um dos quais a função tem inversa.
Passo 1
Fala povo, belezita? Ó só, o nosso gráfico de é esse:
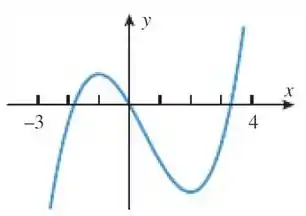
E gente, ta vendo que existem três valores diferentes de que resultam em ? Quando é assim, dizemos que a função não é injetora. Só função bijetora (e logo, injetora) é invertível pessoal, então nesse domínio aí, realmente, nossa não será invertível.
A questão pede mais uma coisinha pra gente: Subdividir o gráfico em três pedaços em que cada pedaço seja invertível. Bem pessoal, de boas, basta a gente cortar o gráfico de forma que cada pedaço seja injetora. Se cortarmos assim:
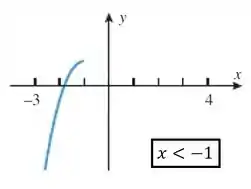
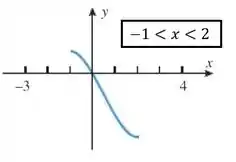
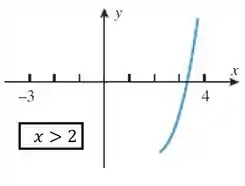
Cada um desses pedaços vai ter somente um associado a cada , ao contrário da função original! Feshow então.
Resposta
A função não é invertível no domínio por não ser injetora no mesmo. Podemos cortar a função em três pedaços, cada qual com seu domínio, de forma que cada pedaço se torne injetora e logo, invertível. Os pedaços são:
