Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 49
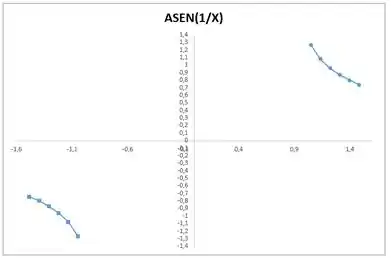
Enfocando conceitos
A função é definida como sendo a inversa da função cotangente restrita:
E a função é definida como sendo a inversa da função cossecante restrita:
Use essas definições em todos os exercícios subsequentes que envolverem essas funções.
- Esboce os gráficos de e
- Obtenha o domínio e a imagem de e
Passo 1
Fala galera, tudo bem? Vamo que vamo! Vamos começar definindo:
Agora a ideia vai ser a gente mexer com essas definições pra que apareçam formas mais familiares pra gente. Como temos funções trigonométricas inversas, pra gente ter uma ideia do esboço, podemos inverter:
O que é o mesmo que:
Trocando as coisas de lado, temos:
E fazendo a inversa trigonométrica, obtemos:
Bem mais tranquilo de esboçar assim né? Afinal, podemos usar as ferramentas de função arco mais conhecidas! As outras nem sequer tem na ferramenta gráfica que vamos usar. Com a ajuda de uma famosa ferramenta de planilhas, usando a função “=ASEN()” e “=ATAN()”, conseguimos esboçar :
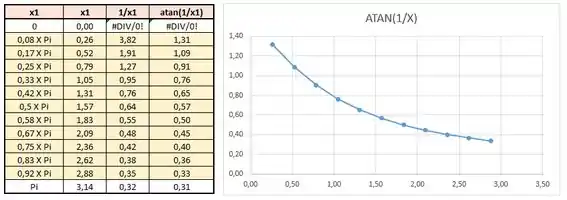
Note que como o intervalo de é , removemos esses pontos, só sendo usados os indicados. Temos também o esboço de , que fica:
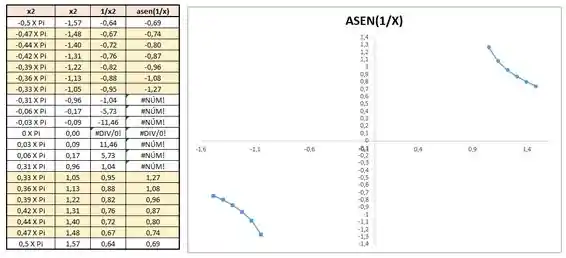
Aqui temos um resultado interessante. Como e são equações análogas e todo seno está limitado por e , tivemos que remover desse gráfico todos os dentro do intervalo que resultassem em . Portanto o gráfico foi feito usando só os pontos indicados, já que os outros não são né parte do domínio de .
Passo 2
E pelo que vimos enquanto construímos esses gráficos, achar o domínio é tranquilo. Seja:
Para:
Vimos que, para a função , o domínio é o mesmo do gráfico montado. Agora, dentro do último intervalo acima, como conversamos, temos pontos fora do domínio de ! O domínio então será o mesmo que pegar isso:
E remover dele os pontos que vimos no final do passo anterior. Isto é:
O resultado vai ser:
Fechemo!
Resposta
Para , temos o seguinte domínio e esboço de gráfico:
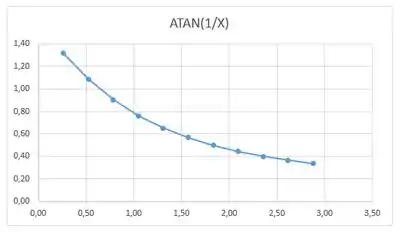
Para , temos o seguinte domínio e esboço de gráfico:
