Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 33
Explique por que o método de Newton falha quando aplicado à equação com qualquer valor inicial . Ilustre sua explicação com um esboço.
Passo 1
E aí! como vai?
Nesse problema foi dada a equação
E nosso objetivo é mostrar que o método de Newton falha quando tentamos aplica-lo nessa equação em um chute inicial .
Tem ideia de como fazemos isso?
Vamos lá aplicar o método de Newton, para isso vamos usar sua fórmula:
Onde é dado por
Vamos começar montando nossa formulinha a partir de , e de um chute inicial (nesse caso diferente de .
Para aplicar o método, temos que ir repetindo os cálculos até encontrar dois resultados iguais ...
Mas nesse caso, o problema já nos disse que isso não é possivel, então vamos aplicar e ver o que acontece...
Bora lá!
Passo 2
Vamos começar montando a formulinha e pre isso precisamos de ...
Pela regra da potência...
Substituindo na nossa formulinha, temos
Vamos simplificar essa fórmula...
Escrevendo as raízes na forma exponencial...
Somando os expoentes do produto , temos
Tranquilo até aqui?
Passo 3
Vamos analisar essa equação...
Cada aproximação sucessiva se torna duas vezes maior que a anterior em valor absoluto, então ela vai falhar em convergir para a raiz, que é , dá pra ver isso direitinho no gráfico abaixo, onde , e .
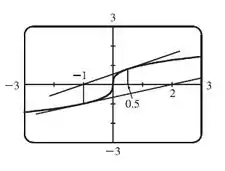
Ou seja, diverge, então para , nossa fórmulinha se distancia cada vez mais da raiz, logo, o método de Newton falha nesse caso!
Interessante, não é? Responde Aí!
Resposta
Cada aproximação sucessiva se torna duas vezes maior que a anterior em valor absoluto, então ela vai falhar em convergir para a raiz.