Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 9

Obtenha gráficos de f que revelem todos os aspectos importantes da curva. Estime os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão, e use o cálculo para achar essas quantidades exatamente.

f x = 1 + 1 x + 8 2 + 1 x 3

Passo 1

Bom galera, nesse exercício estamos interessados em encontrar o intervalo de decrescimento e crescimento da função, os valores extremos, os intervalos de concavidade e os pontos de inflexão. Para isso, iremos utilizar o gráfico da função e o cálculo de derivadas de primeira e segunda ordem.

Passo 2

Derivando f ( x ) em relação a x , temos

f ' x = - 1 x 2 - 16 x 3 - 3 x 4

Derivando f ' ( x ) em relação a x , temos

f ' ' x = 2 x 3 + 48 x 4 + 12 x 5

Podemos então fazer os seguintes gráficos

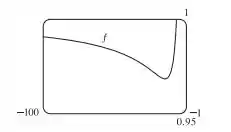
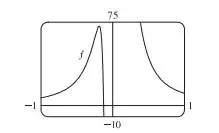
Passo 3

Pelo gráfico, podemos ver que f cresce em ( - 15.8 ,   - 0,2 ) e decresce em ( - ∞ ,   - 15.8 ) , ( - 0.2 ,   0 ) e ( 0 ,   ∞ ) . O valor de mínimo local é f - 15.8 = 0.97 e o valor de Maximo local é f - 0,2 = 72 . Podemos ver que f possui concavidade para baixo em ( - ∞ ,   - 24 ) e ( - 0.25 ,   0 ) e concavidade para cima em ( - 24 ,   - 0.25 ) e ( 0 ,   ∞ ) . Os pontos de inflexão são ( - 24 ,   0.97 ) e ( - 0.25 ,   60 ) . Para encontrar os valores exatos, iremos igualar a primeira e a segunda derivada a zero. Igualando f ' ( x ) a zero, temos

0 = - 1 x 2 - 16 x 3 - 3 x 4

x = - 8 ± 61 = - 0.19   e - 15.81

Igualando f ' ' ( x ) a zero, temos

0 = 2 x 3 + 48 x 4 + 12 x 5

x = - 12 ± 138 = - 0.25   e - 23.75

Resposta

Nossa função está crescendo em ( - 0.19 ,   - 15.81 ) e decrescendo em ( - ∞ ,   - 15.81 ) , ( - 0.2 ,   0 ) e ( 0 ,   ∞ ) . Os pontos de inflexão são ( - 24 ,   0.97 ) e ( - 0.25 ,   60 ) . Nossa função possui concavidade para cima em ( - 23.75 ,   - 0.25 ) e ( 0 ,   ∞ ) e concavidade para baixo em ( - ∞ ,   - 23.75 ) e ( - 0.25 ,   0 ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace ou copie o gráfico de f . (Suponha os eixos com a mesma escala.) Use o método do Exemplo 1 para esboçar o gráfico de f ' .9.
Use um sistema algébrico computacional para fazer o gráfico de f e encontre f ' e f ' ' . Utilize os gráficos dessas derivadas para estimas os intervalos de crescimento, valores extremos, intervalos d
Use um sistema algébrico computacional para fazer o gráfico de f e encontre f ' e f ' ' . Utilize os gráficos dessas derivadas para estimas os intervalos de crescimento, valores extremos, intervalos d
Obtenha os gráficos de f que revelem todos os aspectos importantes da curva. Estime os intervalos de crescimento e decrescimento, valores extremos, intervalos de concaviade e pontos de inflexão, e use
Trace ou copie o gráfico de f . (Suponha os eixos da mesma escala). Use então o método do Exemplo 1 para esboçar o gráfico de f ' .