Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.7 - Ex. 6
Os extremos de uma tina são triângulos equiláteros com lados que medem 60 cm. Se a água na tina tiver 30 cm de profundidade, ache a força devido à pressão do líquido em um extremo.
Passo 1
Se temos uma placa submersa verticalmente em um líquido de densidade , e o comprimento da placa a uma profundidade de unidades puder ser representado por uma função , contínua e positiva no intervalo , então a força causada pela pressão líquida em um lado da placa é:
Devemos primeiro achar uma função que descreva o comprimento da parede da tina em função da profundidade da água, para podermos calcular usando a fórmula.
Passo 2
Conseguimos achar o comprimento em função da profundidade por semelhança de triângulos, como mostra a figura. Se é o lado do triângulo, sua altura é cm.
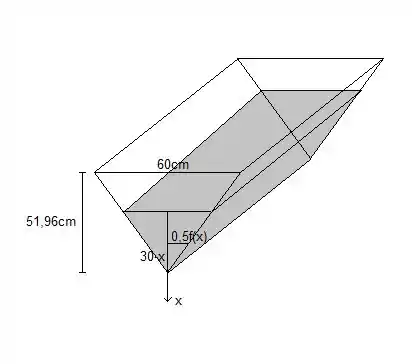
Temos então, por semelhança de triângulos:
Passo 3
Aplicando então a fórmula, com e m:
Para e :