Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 11

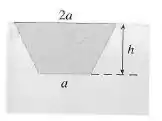
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Então expresse a força como uma integral e calcule-a

Passo 1

Olá, amigo. Yuri aqui e estarei te ajudando a resolver a atividade.

A soma de Riemann podemos dizer que é uma soma de várias pequenas áreas de uma região, e é o surgimento da integração, que tem aplicação em diversas situações, inclusive nessa.

Lembre-se de um fato, a pressão é dada por:

𝑃   =   𝐹 𝐴

Então se podermos calcular as diversas forças das pequenas regiões e com a soma de Reimann calcular a força total.

Passo 2

Podemos ilustrar a situação da seguinte forma

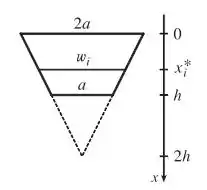
Precisamos calcular w i para podermos encontrar uma expressão para a área, então utilizando de semelhança de triângulos:

w i 2 h - x i * = 2 a 2 h

w i = a h ( 2 h - x i * )

Então, temos que a área é

A = a h 2 h - x i * ∆ x

A pressão é dada por P = ∂ x i * . Então podemos escrever a força como

F = lim n → ∞ ⁡ ∑ i = 1 n ∂ x i * ⋅ a h 2 h - x i * ∆ x

Temos que ∂ = ρ g = 9800   N

Então, podemos escrever como uma integral

𝐹 = ∫ 0 h 𝜕 𝑥 ⋅ 𝑎 h 2 h − 𝑥 𝑑 𝑥 =

𝜕 𝑎 h ∫ 0 h 2 h 𝑥 − 𝑥 2 𝑑 𝑥 =

𝜕 𝑎 h h 𝑥 2 − 𝑥 3 3 = 𝜕 𝑎 h h 3 − h 3 3 = 𝜕 𝑎 h 2 h 3 3 = 2 3 𝜕 𝑎 h 2

Resposta

F = 2 3 ∂ a h 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa tem a forma da região limitada pela parábola x 2 = 6 y e pela reta 2 y = 3 e é colocada num tanque com água tendo o seu vértice voltado para baixo e a reta na superfície da água. Ache a forç
Um tanque cilíndrico está cheio de gasolina com uma densidade de 641k g / m 3 . Se o eixo do cilindro for horizontal e o diâmetro for de 8m , ache a força total sobre um extremo devido à pressão do lí
A base de uma piscina é um plano inclinado. A piscina tem 2m de profundidade em um extremo e 8m no outro. Se a largura da piscina for 25 m e o comprimento for 40m , ache a força total em decorrência d
Uma placa semicircular com um raio de 3m está submersa verticalmente num tanque de agua com o diâmetro na superfície. Encontre a força decorrente da pressão da agua sobre o lado da placaResolva usando
A face de um reservatório adjacente à agua é inclinado 45º em relação a vertical . A face é um retângulo com 80m de comprimento e um lado inclinado de 40m. Se o reservatório está cheio, ache a força t